高中数学一阶、二阶线性常系数递归数列的通项公式试题

已知向量p＝(a_n,2ⁿ)，向量q＝(2^n＋1，－a_n＋1)，n∈N^*，向量p与q垂直，且a₁＝1.
(1)求数列{a_n}的通项公式；
(2)若数列{b_n}满足b_n＝log₂a_n＋1，求数列{a_n·b_n}的前n项和S_n.

对于数列{a_n}，定义数列{a_n＋1－a_n}为数列{a_n}的“差数列”，若a₁＝2，{a_n}的“差数列”的通项为2ⁿ，则数列{a_n}的前n项和S_n＝________.

如图所示，当n≥2时，将若干点摆成三角形图案，每条边(包括两个端点)有n个点，若第n个图案中总的点数记为a_n，则a₁＋a₂＋a₃＋…＋a₁₀＝(　　)

A．126	B．135
C．136	D．140

已知曲线C：y＝ (x>0)及两点A₁(x_1,0)和A₂(x_2,0)，其中x₂>x₁>0.过A₁，A₂分别作x轴的垂线，交曲线C于B₁，B₂两点，直线B₁B₂与x轴交于点A₃(x_3,0)，那么(　　)

A．x1，，x2成等差数列	B．x1，，x2成等比数列
C．x1，x3，x2成等差数列	D．x1，x3，x2成等比数列

S_n是数列{a_n}的前n项和，则“S_n是关于n的二次函数”是“数列{a_n}为等差数列”的(　　)

A．充分不必要条件	B．必要不充分条件
C．充分必要条件	D．既不充分也不必要条件

已知数列{a_n}满足a₁＝a(a＞0，a∈N^*)，a₁＋a₂＋…＋a_n－pa_n＋1＝0(p≠0，p≠－1，n∈N^*)．
(1)求数列{a_n}的通项公式a_n；
(2)若对每一个正整数k，若将a_k＋1，a_k＋2，a_k＋3按从小到大的顺序排列后，此三项均能构成等差数列，且公差为d_k.①求p的值及对应的数列{d_k}．
②记S_k为数列{d_k}的前k项和，问是否存在a，使得S_k＜30对任意正整数k恒成立？若存在，求出a的最大值；若不存在，请说明理由．

已知数列{a_n}的前n项和为S_n，且满足S_n＝n²，数列{b_n}满足b_n＝，T_n为数列{b_n}的前n项和．
(1)求数列{a_n}的通项公式a_n和T_n；
(2)若对任意的n∈N^*，不等式λT_n<n＋(－1)ⁿ恒成立，求实数λ的取值范围．

已知函数f(x)＝的图象过原点，且关于点(－1,2)成中心对称．
(1)求函数f(x)的解析式；
(2)若数列{a_n}满足a₁＝2，a_n＋1＝f(a_n)，试证明数列为等比数列，并求出数列{a_n}的通项公式．

已知等差数列{a_n}满足：a₂＝5，a₄＋a₆＝22，数列{b_n}满足b₁＋2b₂＋…＋2^n－1b_n＝na_n，设数列{b_n}的前n项和为S_n.
(1)求数列{a_n}，{b_n}的通项公式；
(2)求满足13<S_n<14的n的集合．

已知数列{a_n}的前n项和是S_n，且S_n＋a_n＝1.
(1)求数列{a_n}的通项公式；
(2)记b_n＝log₃，数列的前n项和为T_n，证明：T_n<.

第30届奥运会在伦敦举行．设数列a_n＝log_n＋1(n＋2)(n∈N^*)，定义使a₁·a₂·a₃…a_k为整数的实数k为奥运吉祥数，则在区间[1,2 012]内的所有奥运吉祥数之和为________．

已知数列{a_n}的通项公式是a_n＝－n²＋12n－32，其前n项和是S_n，对任意的m，n∈N^*且m<n，则S_n－S_m的最大值是________．

已知数列的前n项和
（1）求数列的通项公式,并证明是等差数列；
（2）若，求数列的前项和

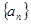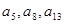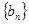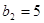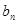数列是公差不为零的等差数列，并且是等比数列的相邻三项，若，则等于（   ）

A．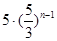

B．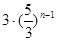

C．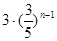

D．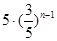

设关于x的不等式x²－x＜2nx(n∈N^*)的解集中整数的个数为a_n，数列{a_n}的前n项和为S_n，则的值为________．