已知函数 (a是常数,a∈R)
(a是常数,a∈R)
(1)当a=1时求不等式 的解集.
的解集.
(2)如果函数 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.
已知函数 .
.
(1)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分12分)
已知函数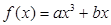 ,曲线
,曲线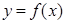 在点
在点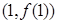 处的切线方程为
处的切线方程为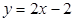 .
.
(1)求函数 的解析式;
的解析式;
(2)过点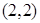 能作几条直线与曲线
能作几条直线与曲线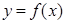 相切?说明理由.
相切?说明理由.
利用二分法求方程x2-2=0的一个正根的近似值.(精确到0.1)
.已知函数 (
( 为常数),直线l与函数
为常数),直线l与函数 的图象都相切,且l与函数
的图象都相切,且l与函数 的图象的切点的横坐标为1.
的图象的切点的横坐标为1.

(1)求直线l的方程及a的值;(2)当k>0时,试讨论方程 的解的个数.
的解的个数.
已知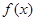 对一切实数
对一切实数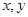 都有
都有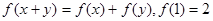 ,当
,当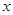 >
> 时,
时,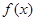 <
< .
.
(1)证明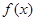 为奇函数
为奇函数
(2)证明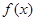 为
为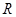 上的减函数
上的减函数
(3)解不等式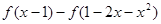 <
<