已知函数 ;
; .
.
(I)当 时,求函数f(x)在
时,求函数f(x)在 上的值域;
上的值域;
(II)若对任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(Ⅲ)若 (
( 为常数),且对任意
为常数),且对任意 ,总有
,总有 成立,求M的取值范围.
成立,求M的取值范围.
根据统计,组装第x件某产品( ),甲工人所用的时间为
),甲工人所用的时间为 ,乙工人所用的时间为
,乙工人所用的时间为 (
( ,
, 为常数)(单位:分钟).已知乙工人组装第4件产品用时15分钟,组装第
为常数)(单位:分钟).已知乙工人组装第4件产品用时15分钟,组装第 件产品用时10分钟.
件产品用时10分钟.
(Ⅰ)求 和
和 的值;
的值;
(Ⅱ)组装第x件某产品,甲工人的用时是否可能多于乙工人的用时?若可能,求出所有x的值;若不可能,请说明理由.
(本题满分14分,第1小题满分4分,第2小题满分4分,第3小题满分6分)
设函数 ,
,
(1)求 的反函数
的反函数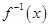 ;
;
(2)判断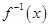 的单调性,不必证明;
的单调性,不必证明;
(3)令 ,当
,当

 ,
, 时,
时,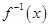 在
在 上的值域是
上的值域是 ,求
,求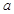 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求满足
时,求满足 的
的 的取值范围;
的取值范围;
(2)若 的定义域为R,又是奇函数,求
的定义域为R,又是奇函数,求 的解析式,判断其在R上的单调性并加以证明.
的解析式,判断其在R上的单调性并加以证明.
本小题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
设函数 是定义域为R的奇函数.
是定义域为R的奇函数.
(1)求k值;
(2)(文)当 时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
时,试判断函数单调性并求不等式f(x2+2x)+f(x-4)>0的解集;
(理)若f(1)<0,试判断函数单调性并求使不等式 恒成立的
恒成立的 的取值范围;
的取值范围;
(3)若f(1)=,且g(x)=a 2x+a - 2x-2m f(x) 在[1,+∞)上的最小值为-2,求m的值.