高中数学随机思想的发展解答题

2012年3月2日，江苏卫视推出全新益智答题类节目《一站到底》，甲、乙两人报名参加《一站到底》面试的初试选拔，已知在备选的10道试题中，甲能答对其中的6题，乙能答对其中的8题．规定每次抢答都从备选题中随机抽出3题进行测试，至少答对2题初试才能通过．
（Ⅰ）求甲答对试题数ξ的概率分布及数学期望；
（Ⅱ）求甲、乙两人至少有一人初试通过的概率．

在某校高三学生的数学校本课程选课过程中，规定每位同学只能选一个科目。已知某班第一小组与第二小组各 有六位同学选择科目甲或科 目乙，情况如下表：

	科目甲	科目乙	总计
第一小组	1	5	6
第二小组	2	4	6
总计	3	9	12

现从第一小组、第二小 组中各任选2人分析选课情况.
（1）求选出的4 人均选科目乙的概率；
（2）设为选出的4个人中选科目甲的人数，求的分布列和数学期望．

某品牌汽车4S店对最近100位采用分期付款的购车者进行统计，统计结果如下表所示：

付款方式	分1期	分2期	分3期	分4期	分5期
频数	40	20		10

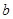已知分3期付款的频率为0.2，4s店经销一辆该品牌的汽车，顾客分1期付款，其利润为1万元，分2期或3期付款其利润为1.5万元，分4期或5期付款，其利润为2万元，用Y表示经销一辆汽车的利润。
(Ⅰ)求上表中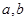的值;
(Ⅱ)若以频率作为概率，求事件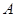：“购买该品牌汽车的3位顾客中，至多有一位采用3期付款”的概率;
（Ⅲ）求Y的分布列及数学期望EY．

在平面内，不等式确定的平面区域为，不等式组确定的平面区域为.
（1）定义横、纵坐标为整数的点为“整点”. 在区域中任取3个“整点”，求这些“整点”中恰好有2个“整点”落在区域中的概率；
（2）在区域中每次任取一个点，连续取3次，得到3个点，记这3个点落在区域中的个数为，求的分布列和数学期望．

某中学校本课程共开设了A，B，C，D共4门选修课，每个学生必须且只能选修1门选修课，现有该校的甲、乙、丙3名学生：
（1）求这3名学生选修课所有选法的总数；
（2）求恰有2门选修课没有被这3名学生选择的概率；
（3）求A选修课被这3名学生选择的人数的数学期望.

小王参加一次比赛,比赛共设三关,第一、二关各有两个必答题,如果每关两个问题都答对,可进入下一关,第三关有三个问题,只要答对其中两个问题,则闯关成功.每过一关可一次性获得价值分别为1000元,3000元,6000元的奖品(不重复得奖),小王对三关中每个问题回答正确的概率依次为,且每个问题回答正确与否相互独立.
(1)求小王过第一关但未过第二关的概率;
(2)用X表示小王所获得奖品的价值,写出X的概率分布列,并求X的数学期望.

张师傅驾车从公司开往火车站，途径4个公交站，这四个公交站将公司到火车站
分成5个路段，每个路段的驾车时间都是3分钟，如果遇到红灯要停留1分钟，假设他在各
交通岗是否遇到红灯是相互独立的，并且概率都是
（1）求张师傅此行时间不少于16分钟的概率
（2）记张师傅此行所需时间为Y分钟，求Y的分布列和均值

已知甲盒内有大小相同的1个红球和3个黑球， 乙盒内有大小相同的2个红球和4个黑球，现从甲、乙两个盒内各任取2个球．
（Ⅰ）求取出的4个球均为黑球的概率；
（Ⅱ）求取出的4个球中恰有1个红球的概率；
（Ⅲ）设为取出的4个球中红球的个数，求的分布列和数学期望．

（本上题满分12分）某高校为了参加“CBA杯”安徽省大学生篮球联赛暨第十届CU—BA安徽省选拔赛，需要在各班选拔预备队员，规定投篮成绩甲级的可作为入围选手，选拔过程中每人投篮5次，若投中3次则确定为乙级，若投中4次及以上则可确定为甲级，一旦投中4次，即终止投篮，已知某班同学小明每次投篮投中的概率是0.6。（I）求小明投篮4次才被确定为乙级的概率； （II）设小明投篮投中次数为X，求X的分布列及期望。

甲、乙等五名奥运志愿者被随机地分到四个不同的岗位服务，每个岗位至少有一名志愿者．（Ⅰ）求甲、乙两人同时参加岗位服务的概率；（Ⅱ）求甲、乙两人不在同一个岗位服务的概率；（Ⅲ）设随机变量为这五名志愿者中参加岗位服务的人数， 可取何值？请求出相应的值的分布列．

(本题满分12分)一厂家向用户提供的一箱产品共件，其中有件次品，用户先对产品进行抽检以决定是否接收．抽检规则是这样的：一次取一件产品检查（取出的产品不放回箱子），若前三次没有抽查到次品，则用户接收这箱产品；若前三次中一抽查到次品就立即停止抽检，并且用户拒绝接收这箱产品.
（Ⅰ）求这箱产品被用户接收的概率；
（Ⅱ）记抽检的产品件数为，求随机变量的分布列和数学期望．

（本小题共13分）
　　一厂家向用户提供的一箱产品共10件，其中有2件次品，用户先对产品进行抽检以决定是否接收。抽检规定是这样的：一次取一件产品检查，若前三次没有抽查到次品，则用户接收这箱产品，而前三次中只要抽查到次品就停止抽检，并且用户拒绝接收这箱产品。
　　（I）求这箱产品被用户拒绝接收的概率；
　　（II）记表示抽检的产品件数，求的概率分布列。

(2009湖南卷理)（本小题满分12分）  
为拉动经济增长，某市决定新建一批重点工程，分别为基础设施工程、民生工程和产业建设工程三类，这三类工程所含项目的个数分别占总数的.、、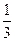，现在3名工人独立地从中任选一个项目参与建设。          
（I）求他们选择的项目所属类别互不相同的概率；
（II）记为3人中选择的项目属于基础设施工程、民生工程和产业建设工程的人数，求 的分布列及数学期望。

2009全国卷Ⅱ理（本小题满分12分）
某车间甲组有10名工人，其中有4名女工人；乙组有5名工人，其中有3名女工人，现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两组中共抽取3名工人进行技术考核。
（I）求从甲、乙两组各抽取的人数；     
（II）求从甲组抽取的工人中恰有1名女工人的概率；
（III）记表示抽取的3名工人中男工人数，求的分布列及数学期望。             

（本小题满分12分）甲、乙等五名环保志愿者被随机地分到四个不同的岗位服务，每个岗位至少有一名志愿者．
（1）求甲、乙两人同时参加岗位服务的概率；
（2）求甲、乙两人不在同一个岗位服务的概率；
（3）设随机变量为这五名志愿者中参加岗位服务的人数，求的分布列．