高中数学随机思想的发展填空题

某车站每天都恰有一辆客车到站，但到站的时刻是随机的，且两者到站的时间是相互独立的，其规律为

到站的时刻	8：10 9：10	8：30 9：30	8：50 9：50
概率

一旅客8：20到站，则它候车时间的数学期望为＿＿＿＿＿＿＿。（精确到分）

一组数据为，，10，11，9，这组数据平均数为10，则方差的最小值为.

一个盒中有9个正品和3个废品，每次取一个产品，取出后不在放回，在取得正品前已取出的废品数的数学期望=_________________.

从集合的所有非空子集中，等可能地取出一个.
（理）记所取出的非空子集中元素的个数为，则的数学期望=.
（文）取出的非空子集中所有元素之和恰为6的概率=.

从1，2，3，，，这个数中任取两个数，设这两个数之积的数学期望为，则________.

某人5 次上班所花的时间（单位：分钟）分别为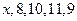，若这组数据的平均数为10，则其方差为 ▲.

一只不透明的布袋中装有编号为1、2、3、4、5的五个大小形状完全一样的小球，现从袋中同时摸出只小球，用随机变量表示摸出的只球中的最大号码数，则随机变量的数学期望．

设是离散型随机变量，，且，又，则的值为_______．

据IEC（国际电工委员会）调查显示，小型风力发电项目投资较少，且开发前景广阔，但受风力自然资源影响，项目投资存在一定风险.根据测算，风能风区分类标准如下：

假设投资A项目的资金为（≥0）万元，投资B项目资金为（≥0）万元，调研结果是：未来一年内，位于一类风区的A项目获利的可能性为，亏损的可能性为；位于二类风区的B项目获利的可能性为，亏损的可能性是，不赔不赚的可能性是.
（1）记投资A，B项目的利润分别为和，试写出随机变量与的分布列和期望，；
（2）某公司计划用不超过万元的资金投资于A，B项目，且公司要求对A项目的投资不得低于B项目,根据（1）的条件和市场调研，试估计一年后两个项目的平均利润之和的最大值．

设非零常数d是等差数列的公差，随机变量等可能地取值，则方差

设随机变量,则.

某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为 $\frac{2}{3}$，得到乙、丙公司面试的概率均为 $P$，且三个公司是否让其面试是相互独立的．记 $X$为该毕业生得到面试的公司个数．若 $P(X=0)=\frac{1}{12}$，则随机变量 $X$的数学期望 $E\left(X\right)=$．

某市有一个玉米种植基地．该基地的技术员通过种植实验发现，一种品质优良的玉米种子每粒发芽的概率都为0.95，现在该种植基地播种了10000粒这种玉米种子，对于没有发芽的种子，每粒需再播种1粒，补种的种子数记为，则的数学期望 .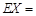

某学生在参加政、史、地三门课程的学业水平考试中，取得A等级的概率分别为、、，且三门课程的成绩是否取得A等级相互独立．记ξ为该生取得A等级的课程数，其分布列如表所示，则数学期望E(ξ)的值为________．

ξ	0	1	2	3
P		a	b

小李练习射击，每次击中目标的概率为，用表示小李射击次击中目标的次数，则的均值与方差的值分别是______________________．