如图所示,四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,M、N分别是AB、PC的中点,PA=AD=a.
(1)求证:MN∥平面PAD;
(2)求证:平面PMC⊥平面PCD.
在四棱锥 中,
中, 底面
底面 ,
, ,
, ,
, ,
, ,
, 是
是 的中点.
的中点.
(1) 证明: ;
;
(2) 证明: 平面
平面 ;
;
(3) 求二面角 的余弦值.
的余弦值.
如图,在五面体 中,已知
中,已知 平面
平面 ,
, ,
, ,
, ,
, .
.
(1)求证: ;
;
(2)求三棱锥 的体积.
的体积.
(本小题8分)如图,在直三棱柱  中,AB=AC,D、E分别是棱BC、
中,AB=AC,D、E分别是棱BC、  上的点(点D不在BC的端点处),且AD
上的点(点D不在BC的端点处),且AD DE,F为
DE,F为  的中点.
的中点.
(1)求证:平面ADE 平面
平面 ;
;
(2)求证: 平面ADE.
平面ADE.
(本小题满分13分)
如图,⊙O在平面 内,AB是⊙O的直径,
内,AB是⊙O的直径, 平面
平面 ,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 ;
;
(3)求证: 平面
平面 .
.
如图,四棱锥 ,平面
,平面 ⊥平面
⊥平面 ,△
,△ 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且 .
.
(1)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为
为 上任意一点,试问点
上任意一点,试问点 在线段
在线段 上什么位置时,
上什么位置时, ⊥
⊥ ;
;
(3)若点 是
是 的中点,求
的中点,求 .
.
如图,四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD.
(1)求证:AB⊥PD;
(2)若M为PC的中点,求证:PA∥平面BDM.
(本小题满分14分)如图,在四面体 中,平面
中,平面
 平面
平面 ,
, 90°.
90°. ,
, ,
, 分别为棱
分别为棱 ,
, ,
, 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面
 平面
平面 .
.
如图,三棱柱 中,
中, 平面ABC,AB
平面ABC,AB BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.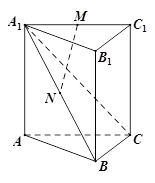
(Ⅰ)求证:MN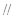 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC 平面A1ABB1.
平面A1ABB1.
如图,三棱锥 中,
中, 平面
平面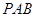 ,
,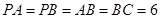 ,点
,点 ,
, 分别为
分别为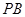 ,
, 的中点.
的中点.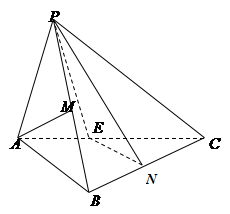
(1)求证: 平面
平面 ;
;
(2) 在线段
在线段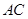 上的点,且
上的点,且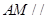 平面
平面 .
.
①确定点 的位置;
的位置;
②求直线 与平面
与平面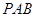 所成角的正切值.
所成角的正切值.
(本小题满分12分)在长方体 中,
中, ,
, .点
.点 是线段
是线段 上的动点,点
上的动点,点 为
为 的中点.
的中点.
(1)当 点是
点是 中点时,求证:直线
中点时,求证:直线 ∥平面
∥平面 ;
;
(2)若二面角 的余弦值为
的余弦值为 ,求线段
,求线段 的长.
的长.
如图,矩形 所在平面与直角三角形
所在平面与直角三角形 所在平面互相垂直,
所在平面互相垂直, ,点
,点 分别是
分别是 的中点.
的中点.
(1)求证:  ∥平面
∥平面 ;
;
(2)求证:平面 平面
平面 .
.