高中数学误差估计解答题

某电视台举办了“中华好声音”大型歌手选秀活动，过程分为初赛、复赛和决赛，经初赛进入复赛的40名选手被平均分成甲、乙两个班，由组委会聘请两位导师各负责一个班进行声乐培训。下面是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图：

赛制规定：参加复赛的40名选手中，获得的支持票数排在前5名的选手可进入决赛，若第5名出现并列，则一起进入决赛；另外，票数不低于95票的选手在决赛时拥有“优先挑战权”。
1、从进入决赛的选手中随机抽出3名，求其中恰有1名拥有“优先挑战权”的概率；
2、电视台决定，复赛票数不低于85票的选手将成为电视台的“签约歌手”，请填写下面的2×2列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成为‘签约歌手’与选择的导师有关？

	甲班	乙班	合计
签约歌手
末签约歌手
合计

下面临界值表仅供参考：

P（K^2≥k）	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	2.072	2.706	3.841	5.024	6.635	7.879	10.828

参考公式：K²= ,其中

某校从参加高一年级期末考试的学生中抽出60名学生，将其物理成绩（均为整数）分成六段，…后画出如下频率分布直方图.观察图形的信息，回答下列问题：
（Ⅰ）估计这次考试的众数m与中位数n（结果保留一位小数）；
(Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分.

（本小题满分14分）下面的茎叶图记录了甲、乙两代表队各10名同学在一次英语听力比赛中的成绩（单位:分）．已知甲代表队数据的中位数为76，乙代表队数据的平均数是75．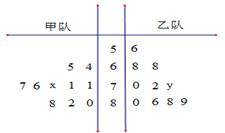

（1）求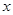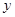，的值；
（2）若分别从甲、乙两队随机各抽取1名成绩不低于80分的学生，求抽到的学生中，甲队学生成绩不低于乙队学生成绩的概率；
（3）判断甲、乙两队谁的成绩更稳定，并说明理由（方差较小者稳定）．

（本小题满分13分）为了调查甲、乙两个网站受欢迎的程度，随机选取了14天，统计上午8：00—10：00间各自的点击量，得如下所示的统计图，根据统计图：
（1）甲、乙两个网站点击量的极差分别是多少？  
（2）甲网站点击量在[10，40]间的频率是多少？  
（3）甲、乙两个网站哪个更受欢迎？并说明理由。

（理科）（本小题满分12分）PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，根据现行国家标准GB3095 – 2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本，监测值频数如下表所示：

PM2.5日均值 （微克/立方米）	[25,35]	(35,45]	(45,55]	(55,65]	(65,75]	(75,85]
频数	3	1	1	1	1	3

（1）从这10天的PM2.5日均值监测数据中，随机抽取3天，求恰有1天空气质量达到一级的概率；（2）从这10天的数据中任取3天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列；（3）以这10天的PM2.5日均值来估计一年的空气质量状况，则一年（按366天算）中平均有多少天的空气质量达到一级或二级。（精确到整数）

)为了了解中学生的身高情况，对某校中学生同年龄的若干名女生的身高进行了测量，将所得数据整理后，画出频率分布直方图(如图)，已知图中从左到右五个小组的频率分别为0.017,0.050，0.100,0.133,0.300，第三小组的频数为6(单位：cm)

(1)参加这次测试的学生人数是多少？
(2)身高在哪个范围内的学生人数最多？这一范围内的人数是多少？
(3)如果本次测试身高在154.5 cm以上的为良好，试估计该校学生身高良好率是多少？

某市交管部门为了宣传新交规举办交通知识问答活动，随机对该市15～65岁的人群抽样，回答问题统计结果如图表所示．

组别	分组	回答正确的人数	回答正确的人数占本组的概率
第1组	[15,25)	5	0.5
第2组	[25,35)		0.9
第3组	[35,45)	27
第4组	[45,55)		0.36
第5组	[55,65)	3

 
（1）分别求出的值；
（2）从第2，3，4组回答正确的人中用分层抽样方法抽取6人，则第2，3，4组每组应各抽取多少人?
（3）在（2）的前提下，决定在所抽取的6人中随机抽取2人颁发幸运奖，求：所抽取的人中第2组至少有1人获得幸运奖的概率．

（理科）PM2.5是指悬浮在空气中的空气动力学当量直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物，根据现行国家标准GB3095 – 2012，PM2.5日均值在35微克/立方米以下空气质量为一级；在35微克/立方米 ~ 75毫克/立方米之间空气质量为二级；在75微克/立方米以上空气质量为超标。从某自然保护区2012年全年每天的PM2.5监测值数据中随机地抽取10天的数据作为样本，监测值频数如下表所示：

PM2.5日均值 （微克/立方米）	[25,35]	(35,45]	(45,55]	(55,65]	(65,75]	(75,85]
频数	3	1	1	1	1	3

（1）从这10天的PM2.5日均值监测数据中，随机抽取3天，求恰有1天空气质量达到一级的概率；（2）从这10天的数据中任取3天数据，记ξ表示抽到PM2.5监测数据超标的天数，求ξ的分布列；（3）以这10天的PM2.5日均值来估计一年的空气质量状况，则一年（按366天算）中平均有多少天的空气质量达到一级或二级。（精确到整数）

某工厂对某产品的产量与单位成本的资料分析后有如下数据：

月    份	1	2	3	4	5	6
产量x千件	2	3	4	3	4	5
单位成本y元/件	73	72	71	73	69	68

（Ⅰ）求单位成本y与月产量x之间的线性回归方程．（其中已计算得：，结果保留两位小数）
（Ⅱ）当月产量为12千件时,单位成本是多少?

对甲、乙两名自行车赛手在相同条件下进行了6次测试，测得他们的最大速度（m/s）的数据如下表．

次数	1	2	3	4	5	6
甲	27	38	30	37	35	31
乙	33	29	38	34	28	36

（1）画出茎叶图，由茎叶图判断哪位选手的成绩较稳定？
（2）分别求出甲、乙两名自行车赛手最大速度（m/s）数据的平均数、中位数、标准差，并判断选谁参加
比赛更合适．

以下茎叶图记录了甲、乙两名射击运动员训练的成绩（环数），射击次数为4次．

（1）试比较甲、乙两名运动员射击水平的稳定性；
（2）每次都从甲、乙两组数据中随机各选取一个进行比对分析，共选取了4次（有放回选取）．设选取的两个数据中甲的数据大于乙的数据的次数为，求的分布列及数学期望．

（本小题满分10分）某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：

分组	频数
[0，0．5）	4
[0．5，1）	8
[1，1．5）	15
[1．5，2）	22
[2，2．5）	25
[2．5，3）	14
[3，3．5）	6
[3．5，4）	4
[4，4．5]	2
合计	100

 
（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？

如图是校园“十佳歌手”大奖赛上，七位评委为甲、乙两位选手打出的分数的茎叶图.

（1）写出评委为乙选手打出分数数据的众数，中位数；
（2）求去掉一个最高分和一个最低分后，两位选手所剩数据的平均数和方差，根据结果比较，哪位选手的数据波动小？

佛山某中学高三(1)班排球队和篮球队各有名同学,现测得排球队人的身高(单位:)分别是:、、、、、、、、、,篮球队人的身高(单位:)分别是:、、、、、、、、、.

(Ⅰ)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算)；
(Ⅱ)现从两队所有身高超过的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?

学校为了对某课题进行研究，用分层抽样方法从三个年级高一、高二、高三的相关老师中，抽取若干人组成研究小组，有关数据见下表(单位：人).

年级	相关人数	抽取人数
高一	18	x
高二	36	2
高三	54	y

 
(1)求x,y;
(2)若从高二、高三抽取的人中选2人做专题发言，求这2人都来自高三的概率。