[广东]2014届广东佛山普通高中高三教学质量检测(一)文数学卷
某由圆柱切割获得的几何体的三视图如图所示,其中俯视图是中心角为 的扇形,则该几何体的体积为( )
的扇形,则该几何体的体积为( )
A. |
B. |
C. |
D. |
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
若函数 的一个正数零点附近的函数值用二分法计算,其参考数据如下:
的一个正数零点附近的函数值用二分法计算,其参考数据如下:
| f(1)=-2 |
f(1.5)=0.625 |
f(1.25)=-0.984 |
| f(1.375)=-0.260 |
f(1.4375)=0.162 |
f(1.40625)=-0.054 |
那么方程 的一个最接近的近似根为( )
的一个最接近的近似根为( )
A. B.
B. C.
C. D.
D.
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点,则该椭圆的离心率为( )
A. |
B. |
C. |
D. |
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
将 个正整数
个正整数 、
、 、
、 、…、
、…、 (
( )任意排成
)任意排成 行
行 列的数表.对于某一个数表,计算各行和各列中的任意两个数
列的数表.对于某一个数表,计算各行和各列中的任意两个数 、
、 (
( )的比值
)的比值 ,称这些比值中的最小值为这个数表的“特征值”.当
,称这些比值中的最小值为这个数表的“特征值”.当 时,数表的所有可能的“特征值”最大值为
时,数表的所有可能的“特征值”最大值为
A. |
B. |
C. |
D. |
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
一个总体分为甲、乙两层,用分层抽样方法从总体中抽取一个容量为 的样本.已知乙层中每个个体被抽到的概率都为
的样本.已知乙层中每个个体被抽到的概率都为 ,则总体中的个体数为 .
,则总体中的个体数为 .
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
佛山某中学高三(1)班排球队和篮球队各有 名同学,现测得排球队
名同学,现测得排球队 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 ,篮球队
,篮球队 人的身高(单位:
人的身高(单位: )分别是:
)分别是: 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 、
、 .
.
(Ⅰ)请把两队身高数据记录在如图所示的茎叶图中,并指出哪个队的身高数据方差较小(无需计算);
(Ⅱ)现从两队所有身高超过
 的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
的同学中随机抽取三名同学,则恰好两人来自排球队一人来自篮球队的概率是多少?
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
如图1,矩形 中,
中, ,
, ,
, 、
、 分别为
分别为 、
、 边上的点,且
边上的点,且 ,
, ,将
,将 沿
沿 折起至
折起至 位置(如图2所示),连结
位置(如图2所示),连结 、
、 ,其中
,其中 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)在线段 上是否存在点
上是否存在点 使得
使得 平面
平面 ?若存在,求出点
?若存在,求出点 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
(Ⅲ)求点 到平面
到平面 的距离.
的距离.
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
数列 、
、 的每一项都是正数,
的每一项都是正数, ,
, ,且
,且 、
、 、
、 成等差数列,
成等差数列, 、
、 、
、 成等比数列,
成等比数列, .
.
(Ⅰ)求 、
、 的值;
的值;
(Ⅱ)求数列 、
、 的通项公式;
的通项公式;
(Ⅲ)记 ,证明:对一切正整数
,证明:对一切正整数 ,有
,有 .
.
来源:2014届广东佛山普通高中高三教学质量检测(一)文数学卷
 的定义域
的定义域 ,
, ,则
,则 ( )
( )



 ,
, 为虚数单位,若
为虚数单位,若 ,则实数
,则实数 ( )
( )



 的最小正周期为
的最小正周期为 ,最大值为
,最大值为 ,则( )
,则( ) ,
,
 ,
,
 ,
, ,且
,且 ,则向量
,则向量 与
与 夹角的大小为( )
夹角的大小为( )



 :若
:若 ,则
,则 ; 命题
; 命题 :若
:若 ,则
,则 .则下列各命题中,假命题的是( )
.则下列各命题中,假命题的是( )



 的值为
的值为 ,则输出的
,则输出的 的值为( )
的值为( )




 .若
.若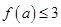 ,则
,则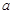 的取值范围是 .
的取值范围是 . 满足
满足 ,若直线
,若直线 将可行域分成面积相等的两部分,则实数
将可行域分成面积相等的两部分,则实数 的值为______.
的值为______.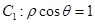 与
与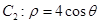 的交点分别为
的交点分别为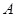 、
、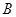 ,则
,则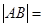 .
. 外一点
外一点 引圆的切线
引圆的切线 和割线
和割线 ,已知
,已知 ,
, ,圆
,圆 ,则圆心
,则圆心 的距离为 .
的距离为 .
 中,角
中,角 、
、 、
、 的对边分别为
的对边分别为 、
、 、
、 ,且
,且 ,
, .
. 的值;
的值; ,求
,求 的值.
的值. .
. ,求
,求 在点
在点 处的切线方程;
处的切线方程; 粤公网安备 44130202000953号
粤公网安备 44130202000953号