高中数学误差估计解答题

为了让学生了解更多“社会法律”知识，某中学举行了一次“社会法律知识竞赛”，共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩（得分均为整数，满分为100分）进行统计．请你根据尚未完成并有局部污损的频率分布表，解答下列问题：

分组	频数	频率
60.5~70.5	①	0.16
70.5~80.5	10	？②
80.5~90.5	18	0.36
90.5~100.5	③	④
合计	50	1

 
（1）若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为
000，001，002，…，799，试写出第二组第一位学生的编号     ；
（2）填充频率分布表的空格①     ②    ③    ④     并作出频率分布直方图；
（3）若成绩在85.5~95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人？

某校从参加某次知识竞赛的同学中，选取60名同学将其成绩（百分制，均为整数）分成6组后，得到部分频率分布直方图（如图），观察图中的信息，回答下列问题．

(Ⅰ)求分数在[70，80）内的频率，并补全这个频率分布直方图；
(Ⅱ)根据频率分布直方图，估计本次考试的平均分；
(Ⅲ)若从60名学生中随机抽取2人，抽到的学生成绩在[40，70）记0分，记[70，100]记1分，用X表示抽取结束后的总记分，求X的分布列和数学期望。

在对人们休闲的一次调查中，共调查了124人，其中女性70人，男性54人。女性中有43人主要的休闲方式是看电视，另外27人主要的休闲方式是运动；男性中有21人主要的休闲方式是看电视，另外33人主要的休闲方式是运动。
（1）根据以上数据建立一个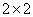的列联表；

P(k^2>k)	0.50	0.40	0.25	0.15	0.10	0.05	0.025	0.010	0.005	0.001
k	0.455	0.708	1.323	2.072	2.706	3.841	5.024	6.635	7.879	10.83

（2）检验性别与休闲方式是否有关系。（本题可以参考两个分类变量x和y有关系的可信度表:）

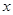	2	4	5	6	8
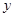	30	40	60	50	70

在某次测验中，有6位同学的平均成绩为75分．用x_n表示编号为n(n＝1,2， ，6)的同学所得成绩，且前5位同学的成绩如下：

编号n	1	2	3	4	5
成绩xn	70	76	72	70	72

(1)求第6位同学的成绩x₆，及这6位同学成绩的标准差s；
(2)从前5位同学中，随机地选2位同学，求恰有1位同学成绩在区间(68,75)中的概率．

以下茎叶图记录了甲、乙两组各四名同学的植树棵树。乙组记录中有一个数据模糊，无法确认，在图中以X表示.

（1）求甲组同学植树棵树的平均数和方差；（参考公式:）
（2）如果X=9，分别从甲、乙两组中随机选取一名同学，求这两名同学的植树总棵数为19的概率.

某校为了解毕业班学业水平考试学生的数学考试情况, 抽取了该校100名学生的数学成绩, 将所有数据整理后, 画出了样频率分布直方图(所图所示), 若第1组、第9组的频率各为.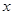

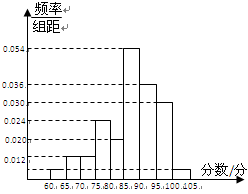
(Ⅰ) 求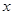的值, 并估计这次学业水平考试数学成绩的平均数;
（Ⅱ）若全校有1500名学生参加了此次考试,估计成绩在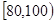分内的人数.

某学生社团在对本校学生学习方法开展问卷调查的过程中发现，在回收上来的1000份有效问卷中，同学们背英语单词的时间安排共有两种：白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响，该社团以5%的比例对这1000名学生按时间安排类型进行分层抽样，并完成一项实验，实验方法是，使两组学生记忆40个无意义音节（如XIQ、GEH），均要求在刚能全部记清时就停止识记，并在8小时后进行记忆测验。不同的是，甲组同学识记结束后一直不睡觉，8小时后测验；乙组同学识记停止后立刻睡觉，8小时后叫醒测验。
两组同学识记停止8小时后的准确回忆（保持）情况如图（区间含左端点而不含右端点）

（1）估计1000名被调查的学生中识记停止后8小时40个音节的保持率大于等于60%的人数；
（2）从乙组准确回忆因结束在[12,24)范围内的学生中随机选3人，记能准确回忆20个以上（含20）的人数为随机变量X，求X分布列及数学期望；
（3）从本次实验的结果来看，上述两种时间安排方法中哪种方法背英语单词记忆效果更好? 计算并说明理由。

中日“钓鱼岛争端”问题越来越引起社会关注，我校对高一600名学生进行了一次“钓鱼岛”
知识测试，并从中抽取了部分学生的成绩（满分100分）作为样本，绘制了下面尚未完成的频率分布表和
频率分布直方图．

（1）填写答题卡频率分布表中的空格，补全频率分布直方图,并标出每个小矩形对应的纵轴数据；
（2）试估计该年段成绩在段的有多少人；
（3）请你估算该年级的平均分.

某中学将100名高一新生分成水平相同的甲、乙两个“平行班”,每班50人.陈老师采用A、B两种不同的教学方式分别在甲、乙两个班级进行教改实验.为了解教学效果,期末考试后,陈老师分别从两个班级中各随机抽取20名学生的成绩进行统计,作出茎叶图如下.记成绩不低于90分者为“成绩优秀”.

(1)在乙班样本的20个个体中,从不低于86分的成绩中随机抽取2个,求抽出的2个至多一个“成绩优秀”的概率；
（2）由以上统计数据填写下面列联表,并判断是否有90%的把握认为：“成绩优秀”与教学方式有关.

	甲班 (A方式）	乙班 (B方式）	总计
成绩优秀
成绩不优秀
总计

附：

	0.25	0.15	0.10	0.05	0.025
k	1.323	2.072	2. 706	3. 841	5. 024

 

(本题满分12分)
为调查某工厂工人生产某种产品的能力，随机抽查了一些工人某天生产产品的数量，产品数量的分组区间为[45,55), [55,65), [65,75), [75,85), [85,95),由此得到频率分布直方图如图所示，保存中不慎丢失一些数据，但已知第一组 （[45,55) ]有4人；

（Ⅰ）求被抽查的工人总人数n及图中所示m为多少；
（Ⅱ）求这些工人中一天生产该产品数量在[55,75)之间的人数是多少。

某校从参加考试的学生中抽出60名学生，将其成绩（均为整数）分成六组[40，50），[50，60） ．．．[90，100]后画出如下部分频率分布直方图.观察图形的信息，回答下列问题：

（Ⅰ）求成绩落在[70，80）上的频率，并补全这个频率分布直方图；
(Ⅱ) 估计这次考试的及格率（60分及以上为及格）和平均分；
(Ⅲ) 从成绩是70分以上（包括70分）的学生中选两人，求他们在同一分数段的概率.

（本小题12分）本某中学为研究学生的身体素质与课外体育锻炼时间的关系，对400名高一学生的一周课外体育锻炼时间进行调查，结果如下表所示：

锻炼时间（分钟）
人数	40	60	80	100	80	40

（1）完成频率分布直方图，并估计该中学高一学生每周参加
课外体育锻炼时间的平均值（同一组中的数据用该区间的组中值作代表）；

（2）现采用分层抽样的方法抽取容量为20的样本，
①应抽取多少名课外体育锻炼时间为分钟的学生；
②若从①中被抽取的学生中随机抽取2名，求这2名学生课外体育锻炼时间均为分钟的概率。

由于当前学生课业负担较重，造成青少年视力普遍下降，现从某高中随机抽取16名学生，经校医检查得到每个学生的视力状况的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶）如图示：

4	3  5  6  6  6  7  7  7  8  8  9  9
5	0  1  1  2

 
指出这组数据的众数和中位数；
若视力测试结果不低于5.0，则称为“健康视力”，求校医从这16人中随机选取3人，至多有1人是“健康视力”的概率；以这16人的样本数据来估计整个学校的总体数据，若从该校（人数很多）任选3人，记表示抽到“健康视力”学生的人数，求的分布列及数学期望

（本小题满分12分）
某大学高等数学老师上学期分别采用了两种不同的教学方式对甲、乙两个大一新生班进行教改试验（两个班人数均为60人，入学数学平均分数和优秀率都相同；勤奋程度和自觉性都一样）。现随机抽取甲、乙两班各20名同学的上学期数学期末考试成绩，得到茎叶图如下：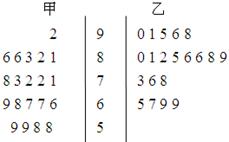

（Ⅰ）依茎叶图判断哪个班的平均分高？
（Ⅱ）从乙班这20名同学中随机抽取两名高等数学成绩不得低于85分的同学，求成绩为90分的同学被抽中的概率；
（Ⅲ）学校规定：成绩不低于85分的为优秀，请填写下面的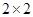列联表，并判断“能否在犯错误的概率不超过0.025的前提下认为成绩优秀与教学方式有关？”

	甲班	乙班	合计
优秀
不优秀
合计

下面临界值表仅供参考：

	0.15	0.10	0.05	0.025	0.010	0.005	0.001
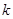	2.072	2.706	3.841	5.024	6.635	7.879	10.828

（参考公式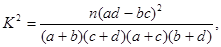：其中）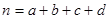 
（Ⅳ）从乙班高等数学成绩不低于85分的同学中抽取2人，成绩不低于90分的同学得奖金100元，否则得奖金50元，记为这2人所得的总奖金，求的分布列和数学期望。

（本小题满分12分）某公司欲招聘员工，从1000名报名者中筛选200名参加笔试，按笔试成绩择优取50名面试，再从面试对象中聘用20名员工．
（1）求每个报名者能被聘用的概率；
（2）随机调查了24名笔试者的成绩如下表所示：

分数段	[60，65)	[65，70)	[70，75)	[75，80)	[80，85)	[85，90)
人数	1	2	6	9	5	1

请你预测面试的分数线大约是多少？
（3）公司从聘用的四男、、、和二女、中选派两人参加某项培训，则选派结果为一男一女的概率是多少？