[四川]2013届四川宜宾高三第二次模拟考试文科数学试卷
在一个几何体的三视图中,正视图和俯视图如下图所示,则该几何体的体积为( )
A.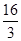 cm3( cm3( |
B. cm3 cm3 |
C. cm3 cm3 |
D.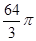 cm3 cm3 |
设 是直线,
是直线, 是两个不同的平面,下列命题成立的是( )
是两个不同的平面,下列命题成立的是( )
A.若 ,则 ,则 |
B.若 ∥ ∥ ,则 ,则 |
C.若 ∥ ∥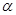 , ,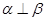 , 则 , 则 ∥ ∥ |
D.若 ∥ ∥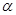 , ,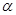 ∥ ∥ ,则 ,则 ∥ ∥ |
函数 (其中A>0,
(其中A>0,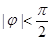 )的图象如图所示,为了得到
)的图象如图所示,为了得到 的图象,则只需将g(x)=sin2x的图象
的图象,则只需将g(x)=sin2x的图象
A.向右平移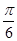 个长度单位 个长度单位 |
B.向左平移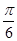 个长度单位 个长度单位 |
C.向右平移 个长度单位 个长度单位 |
D.向左平移 个长度单位 个长度单位 |
设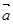 、
、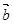 为非零向量,则“
为非零向量,则“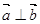 ”是“函数
”是“函数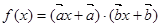 是一次函数”的( )
是一次函数”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知抛物线C: , 直线
, 直线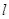 过抛物线C的焦点,且与C的交点为A、B两点,则
过抛物线C的焦点,且与C的交点为A、B两点,则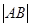 的最小值为( )
的最小值为( )
(A)6 (B)12 (C)18 (D)24
某私立校共有3600人,其中高中部、初中部、小学部的学生人数成等差数列递增,已知公差为600, 现在按1:100的抽样比,用分层抽样的方法抽取样本,则应抽取小学部学生人数为 .
已知平面直角坐标系xoy上的区域D由不等式组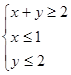 给定,若
给定,若 为D上的动点,A的坐标为(-1,1),则
为D上的动点,A的坐标为(-1,1),则 的取值范围是_____________.
的取值范围是_____________.
在平面直角坐标系xoy两轴正方向有两点A (a, 0)、B(0, b)(a>2, b>2), 线段AB和圆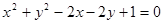 相切, 则△AOB的面积最小值为_____________.
相切, 则△AOB的面积最小值为_____________.
已知函数 的图像上两相邻最高点的坐标分别为
的图像上两相邻最高点的坐标分别为 .
.
(Ⅰ)求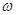 的值;
的值;
(Ⅱ)在△ABC中, 分别是角A,B,C的对边,且
分别是角A,B,C的对边,且 求
求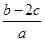 的取值范围.
的取值范围.
如图,在三棱锥P-ABC中, AB="AC=4," D、E、F分别为PA、PC、BC的中点, BE="3," 平面PBC⊥平面ABC, BE⊥DF.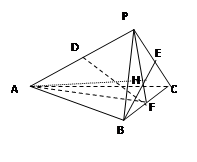
(Ⅰ)求证:BE⊥平面PAF;
(Ⅱ)求直线AB与平面PAF所成的角.
某校为了解毕业班学业水平考试学生的数学考试情况, 抽取了该校100名学生的数学成绩, 将所有数据整理后, 画出了样频率分布直方图(所图所示), 若第1组、第9组的频率各为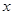 .
.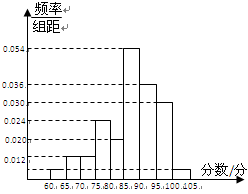
(Ⅰ) 求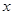 的值, 并估计这次学业水平考试数学成绩的平均数;
的值, 并估计这次学业水平考试数学成绩的平均数;
(Ⅱ)若全校有1500名学生参加了此次考试,估计成绩在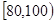 分内的人数.
分内的人数.
设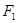 、
、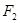 分别为椭圆
分别为椭圆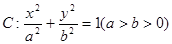 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ) 若椭圆C上的点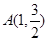 到
到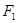 、
、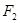 两点的距离之和等于4, 写出椭圆C的方程和离心率.;
两点的距离之和等于4, 写出椭圆C的方程和离心率.;
(Ⅱ) 若M、N是椭圆C上关于原点对称的两点,点P是椭圆上除M、N外的任意一点, 当直线PM、PN的斜率都存在, 并记为 、
、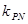 时, 求证:
时, 求证:  ·
·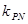 为定值.
为定值.
 ,B=
,B=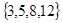 ,C=
,C= ,则可得到( )
,则可得到( )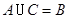
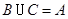
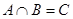
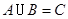
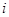 是虚数单位,则
是虚数单位,则 ( )
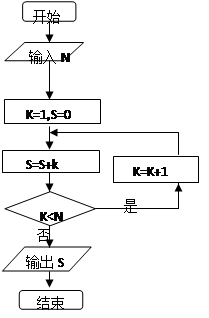
( )
 中,
中, , 则n=( )
, 则n=( ) ,且函数
,且函数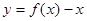 恰有3个不同的零点,则实数
恰有3个不同的零点,则实数 的取值范围是
的取值范围是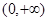
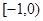
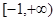

 (
(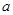 >0)的离心率为
>0)的离心率为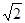 ,则
,则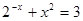 的实数解的个数为_______.
的实数解的个数为_______.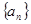 中,
中, 为常数,
为常数,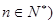 ,且
,且 成公比不等于1的等比数列.
成公比不等于1的等比数列.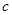 的值;
的值;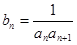 ,求数列
,求数列 的前
的前 项和
项和 。
。 ,当
,当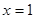 时函数
时函数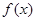 取得一个极值,其中
取得一个极值,其中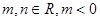 .
.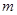 与
与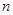 的关系式;
的关系式;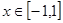 时,函数
时,函数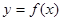 的图象上任意一点的切线的斜率恒大于
的图象上任意一点的切线的斜率恒大于 ,求
,求 粤公网安备 44130202000953号
粤公网安备 44130202000953号