在某次测验中,有6位同学的平均成绩为75分.用xn表示编号为n(n=1,2, ,6)的同学所得成绩,且前5位同学的成绩如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 成绩xn |
70 |
76 |
72 |
70 |
72 |
(1)求第6位同学的成绩x6,及这6位同学成绩的标准差s;
(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
相关知识点
推荐套卷
 作直线
作直线 交曲线
交曲线 :
: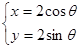 (
(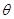 为参数)于
为参数)于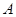 、
、 两点,若
两点,若 成等比数列,求直线
成等比数列,求直线 中,底面
中,底面 为平行四边形,
为平行四边形, ,
, ,
, ⊥底面
⊥底面 平面
平面 ; ②若二面角
; ②若二面角 为
为 ,求
,求 与平面
与平面 所成角的正弦值.
所成角的正弦值.
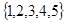 的所有非空子集中,等可能地取出一个.
的所有非空子集中,等可能地取出一个. 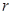 :集合中的所有元素之和为10,求所取出的非空子集满足性质
:集合中的所有元素之和为10,求所取出的非空子集满足性质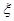 ,求
,求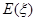 .
.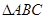 中,角
中,角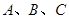 的对边分别为
的对边分别为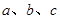 ,且
,且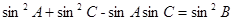 .
. 的大小;
的大小;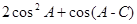 的取值范围.
的取值范围.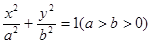 的右焦点为
的右焦点为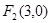 ,离心率为
,离心率为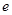 .
.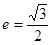 ,求椭圆的方程; (2)设直线
,求椭圆的方程; (2)设直线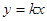 与椭圆相交于
与椭圆相交于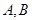 两点,
两点,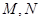 分别为线段
分别为线段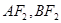 的中点.若坐标原点
的中点.若坐标原点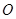 在以
在以 为直径的圆上,且
为直径的圆上,且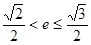 ,求
,求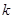 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号