如图,在三棱锥 中,
中, ,
, ,点
,点 ,
, 分别为
分别为 ,
, 的中点.
的中点.

(1)求证:直线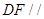 平面
平面 ;
;
(2)求证:
 .
.
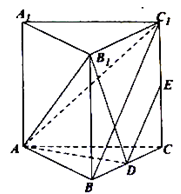
如图,已知直三棱柱 中,
中, ,
, 、
、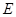 分别为
分别为 、
、 中点,
中点, .
.
(1)求证: 平面
平面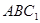 ;
;
(2)求证:平面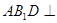 平面
平面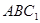
如图,在四棱锥 中,已知底面
中,已知底面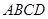 为矩形,
为矩形, 平面
平面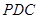 ,点
,点 为棱
为棱 的中点,求证:
的中点,求证:
(1) 平面
平面 ;
;
(2)平面 平面
平面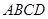 .
.
如图,在直四棱柱ABCD﹣A1B1C1D1中, E,F分别是AB,BC的中点,A1C1与B1D1交于点O.
(1)求证:A1,C1,F,E四点共面;
(2)若底面ABCD是菱形,且 A1E,求证:
A1E,求证: 平面A1C1FE.
平面A1C1FE.
如图,已知直三棱柱 的侧面
的侧面 是正方形,点
是正方形,点 是侧面
是侧面 的中心,
的中心, ,
, 是棱
是棱 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求证:平面 平面
平面 .
.
设 、
、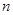 是两条不同的直线,
是两条不同的直线, 、
、 是两个不同的平面,则下列命题中正确的命题是( )
是两个不同的平面,则下列命题中正确的命题是( )
A.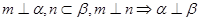 |
B. |
C. |
D. |
如图,在三棱锥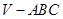 中,平面
中,平面 平面
平面 ,
, 为等边三角形,
为等边三角形, 且
且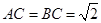 ,
, ,
, 分别为
分别为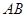 ,
,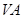 的中点.
的中点.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求证:平面 平面
平面 ;
;
(Ⅲ)求二面角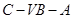 的平面角的余弦值..
的平面角的余弦值..
如图, 是正方体
是正方体 的棱
的棱 的中点,给出下列命题
的中点,给出下列命题
①过 点有且只有一条直线与直线
点有且只有一条直线与直线 ,
, 都相交;
都相交;
②过 点有且只有一条直线与直线
点有且只有一条直线与直线 ,
, 都垂直;
都垂直;
③过 点有且只有一个平面与直线
点有且只有一个平面与直线 ,
, 都相交;
都相交;
④过 点有且只有一个平面与直线
点有且只有一个平面与直线 ,
, 都平行.其中真命题是:
都平行.其中真命题是:
| A.①②③ | B.①②④ | C.①③④ | D.②③④ |
如图,三棱柱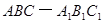 中,
中,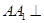 平面ABC,AB
平面ABC,AB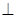 BC , 点M , N分别为A1C1与A1B的中点.
BC , 点M , N分别为A1C1与A1B的中点.
(Ⅰ)求证:MN 平面BCC1B1;
平面BCC1B1;
(Ⅱ)求证:平面A1BC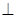 平面A1ABB1.
平面A1ABB1.