如图02,在长方体ABCD-A1B1C1D1中,P、Q、R分别是棱AA1、BB1、BC上的点,PQ∥AB,C1Q⊥PR,求证:∠D1QR=90°.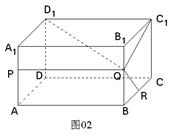
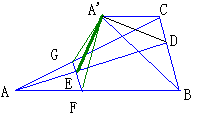
如图在ΔABC中, AD⊥BC,ED=2AE,过E作FG∥BC, 且将ΔAFG沿FG折起,使∠A'ED=60°,求证:A'E⊥平面A'BC
 |
在直四棱柱A1B1C1D1—ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形).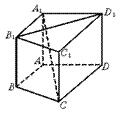
如果一条直线与一个平面垂直,那么,称此直线与平面构成一个“正交线面对”.在一个正方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“正交线面对”的个数是 .
已知∠AOB=90°,过O点引∠AOB所在平面的斜线OC,与OA、OB分别成45°、
60°,则以OC为棱的二面角A—OC—B的余弦值等于______
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,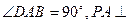 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC= AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。
AB=1,M是PB的中点。(Ⅰ)证明:面PAD⊥面PCD;(Ⅱ)求AC与PB所成的角的余弦值;(Ⅲ)求面AMC与面BMC所成二面角的余弦值。