高中数学空间向量的应用解答题

如图，在直三棱柱中，

（1）求证
（2）在上是否存在点使得
（3）在上是否存在点使得？

如图，正三棱柱的所有棱长都为2，为中点。

（1）求证：面；
（2）求二面角的余弦值；
（3）求点到平面的距离。

如图，已知菱形ACSB中，∠ABS=60°．沿着对角线SA将菱形ACSB折成三棱锥S﹣ABC，且在三棱锥S﹣ABC中，∠BAC=90°，O为BC中点．

（Ⅰ）证明：SO⊥平面ABC；
（Ⅱ）求平面ASC与平面SCB夹角的余弦值．

在梯形ABCD中，AD∥BC，BC=2AD，AD=AB=，AB⊥BC，如图把△ABD沿BD翻折，使得平面ABD⊥平面BCD．

（Ⅰ）求证：CD⊥平面ABD；
（Ⅱ）若点M为线段BC中点，求点M到平面ACD的距离．

如图所示，PA⊥平面ABCD，四边形ABCD为正方形，且E，F，G，H分别是线段PA、PD、CD、BC的中点．

（1）求证：BC∥平面EFG；
（2）DH⊥平面AEG．

如图，四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD为矩形，E，F分别为棱AB，PC的中点

（1）求证：PE⊥BC；
（2）求证：EF∥平面PAD．

如图，△RBC中，RB=BC=2，点A、D分别是RB、RC的中点，且2BD=RC，边AD折起到△PAD位置，使PA⊥AB，连结PB、PC．

（1）求证：BC⊥PB；
（2）求二面角A﹣CD﹣P的平面角的余弦值．

如图所示，在直三棱柱ABC﹣A₁B₁C₁中，AB=BC=BB₁，D为AC的中点．

（I）求证：B₁C∥平面A₁BD；
（Ⅱ）若AC₁⊥平面A₁BD，求证：B₁C₁⊥平面ABB₁A₁；
（Ⅲ）在（II）的条件下，求二面角B﹣A₁C₁﹣D的大小．

矩形与矩形的公共边为，且平面平面，如图所示，，.

（1）证明：平面；
（2）求异面直线与所成角的余弦值；
（3）若是棱的中点，在线段上是否存在一点，使得平面？证明你的结论．

如图，在斜三棱柱中，侧面与侧面都是菱形，，．

（1）求证：；
（2）若，求二面角的正弦值．

如图，棱锥的底面是矩形，⊥平面，．

（1）求证：BD⊥平面PAC；
（2）求二面角P—CD—B的大小；
（3）求点C到平面PBD的距离．

如图所示，四棱锥的底面是直角梯形， ，，，底面，过的平面交于，交于（与不重合）．

（Ⅰ）求证：；
（Ⅱ）如果，求此时的值．

在直三棱柱ABC﹣A₁B₁C₁中，BC=CC₁，AB⊥BC．点M，N分别是CC₁，B₁C的中点，G是棱AB上的动点．

（Ⅰ）求证：B₁C⊥平面BNG；
（Ⅱ）若CG∥平面AB₁M，试确定G点的位置，并给出证明．

在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC=2AD=4，EF=3，AE=BE=2，G是BC的中点．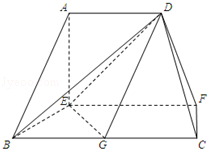

（Ⅰ）求证：AB∥平面DEG；
（Ⅱ）求证：BD⊥EG．

正方形所在的平面与三角形所在的平面交于，且平面．

（1）求证：平面；
（2）求证：平面平面．