高中数学空间向量的应用解答题

如图，四边形ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，
在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：

（本小题满分10分）已知直三棱柱中，，是棱的中点．如图所示．

（1）求证：平面；
（2）求锐二面角的大小．

如图，空间四边形SABC中，SO⊥平面ABC，O为△ABC的垂心。求证：平面SOC ⊥平面SAB。

如图，空间四边形ABCD中，，，分别是AB，BC，CD的中点，求证：

（1）AC∥平面；
（2）BD∥平面．

如图,四棱锥S-ABCD的底面是边长为1的正方形,SD垂直于底面ABCD,SB=

(1)求证:BC⊥SC; (2)设棱SA的中点为M,求证：DM⊥SB.

已知四棱锥的底面是平行四边形，分别是的中点，，，．

（Ⅰ）求证：；
（Ⅱ）若，求二面角的余弦值．

如图，在四棱锥P﹣ABCD中，PA⊥平面ABCD，底面ABCD是菱形，AB=2，∠BAD=60°．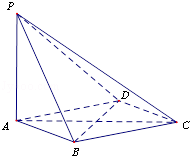

（Ⅰ）求证：BD⊥平面PAC；
（Ⅱ）当平面PBC与平面PDC垂直时，求PA的长．

在空间四边形ABCD中AB⊥CD,AH⊥平面BCD,垂足为H,求证:BH⊥CD。

如图，在三棱柱ABC－A1B1C1中，已知AB⊥侧面BB1C1C，AB＝BC＝1，BB1＝2，∠BCC1＝60°。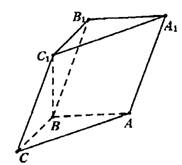

（Ⅰ）求证：C1B⊥平面ABC；
（Ⅱ）设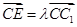（0≤λ≤1），且平面AB1E与BB1E所成的锐二面角的大小为30°，试求λ的值．

如图，正四棱柱中，，点在上且．

（Ⅰ）证明：平面；
（Ⅱ）连结，求二面角的正弦值．

如图，四棱锥P-ABCD，侧面PAD是边长为2的正三角形，且与底面垂直，底面ABCD是∠ABC=60°的菱形，M为PC的中点．

（1）求证：PC⊥AD；
（2）求点D到平面PAM的距离．

（本小题满分12分）
如图，四棱锥中，底面为平行四边形，
，底面 ．

（1）证明：；
（2）求三棱锥的高．

（本小题满分12分）已知三棱柱ABC－中，平面⊥底面ABC，BB′⊥AC，底面ABC是边长为2的等边三角形，＝3，E、F分别在棱，上，且AE＝＝2．

（Ⅰ）求证：⊥底面ABC；
（Ⅱ）在棱上找一点M，使得∥平面BEF，并给出证明．

（本小题满分12分）如图，已知矩形所在的平面与直角梯形所在的平面垂直，且分别为的中点．

（Ⅰ）求证：平面；
（Ⅱ）求证：平面⊥平面．

（本小题满分12分）
四面体ABCD中，对棱AD⊥BC，对棱AB⊥CD，试证明：AC⊥BD.