(本小题满分12分)如图,四棱锥 的底面是正方形,每条侧棱的长都是底面边长的
的底面是正方形,每条侧棱的长都是底面边长的 倍,
倍, 为侧棱
为侧棱 上的点.
上的点.
(1)求证: ;
;
(2)若 平面
平面 ,侧棱
,侧棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ,若存在,确定点
,若存在,确定点 的位置;若不存在,试说明理由.
的位置;若不存在,试说明理由.
(本小题满分12分)如图,正四棱锥 中,
中, .
.
(1)求证: ;
;
(2)在线段 上是否存在点
上是否存在点 ,使得二面角
,使得二面角 的大小为
的大小为 ,若存在,求出
,若存在,求出 ;若不存在,试说明理由.
;若不存在,试说明理由.
如图,在三棱锥 中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若
中,△PAB和△CAB都是以AB为斜边的等腰直角三角形,若 ,D是PC的中点.
,D是PC的中点.
(1)证明:

 ;
;
(2)求AD与平面ABC所成角的正弦值.
如图,在四棱锥P﹣ABCD中,PA⊥底面ABCD,∠DAB为直角,AB∥CD,AD=CD=2AB,E、F分别为PC、CD的中点.
(Ⅰ)试证:AB⊥平面BEF;
(Ⅱ)设PA=k•AB,且二面角E﹣BD﹣C的平面角大于45°,求k的取值范围.
如图,在四棱锥S﹣ABCD中,底面ABCD是正方形,其他四个侧面都是等边三角形,AC与BD的交点为O,E为侧棱SC上一点.
(Ⅰ)当E为侧棱SC的中点时,求证:SA∥平面BDE;
(Ⅱ)求证:平面BDE⊥平面SAC;
(Ⅲ)(理科)当二面角E﹣BD﹣C的大小为45°时,试判断点E在SC上的位置,并说明理由.
(本小题12分)
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AC=BC,D、E、F分别为棱AB、BC、A1C1的中点。
(Ⅰ)证明:EF//平面A1CD;
(Ⅱ)证明:平面A1CD⊥平面ABB1A1。
(本小题满分14分)如图,平面PAC⊥平面ABC,点E、F、O分别为线段PA、PB、AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=2 .求证:
.求证:
(1)PA⊥平面EBO;
(2)FG∥平面EBO.
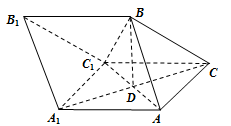
(本小题满分12分)如图,三棱柱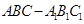 中,
中,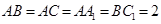 ,
,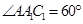 ,平面
,平面 平面
平面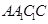 ,
, 与
与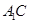 相交于点
相交于点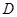 .
.
(Ⅰ)求证: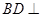 平面
平面 ;
;
(Ⅱ)求二面角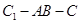 的余弦值.
的余弦值.
(本小题满分12分)在等腰 中,
中, ,
, ,
, 分别是边
分别是边 、
、 的中点,将
的中点,将 沿
沿 翻折,得到四棱锥
翻折,得到四棱锥 ,且
,且 为棱
为棱 中点,
中点, .
.
(1)求证:
 平面
平面 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 ?若存在,求二面角
?若存在,求二面角 的余弦值,若不存在,请说明理由.
的余弦值,若不存在,请说明理由.
如图,在四棱锥P—ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABC是边长为2的菱形,∠BAD=60°,M为PC的中点.
(Ⅰ)求证:PA//平面BDM;
(Ⅱ)在AD上确定一点 ,使得面
,使得面 面
面 ,并加以证明;
,并加以证明;
(Ⅲ)求直线AC与平面ADM所成角的正弦值.
(本小题满分14分)如图,四棱锥 的底面为正方形,侧棱
的底面为正方形,侧棱 底面
底面 ,且
,且 ,
, 分别是线段
分别是线段 的中点.
的中点.
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证: 平面
平面 ;
;
(Ⅲ)求二面角 的大小.
的大小.
(本小题满分12分)如图,四面体 中,
中, 分别
分别 的中点,
的中点, ,
, .
.
(Ⅰ)求证:AO⊥平面 ;
;
(Ⅱ)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求点E到平面ACD的距离.
如图所示,正方形 和矩形
和矩形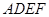 所在平面相互垂直,
所在平面相互垂直,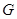 是
是 的中点.
的中点.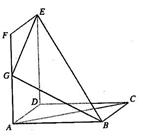
(1)求证: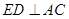 ;
;
(2)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与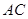 所成角的余弦值.
所成角的余弦值.