直三棱柱 中,
中, ,
, 分别是
分别是 的中点,
的中点, ,
, 为棱
为棱 上的点.
上的点.
(1)证明: ;
;
(2)是否存在一点 ,使得平面
,使得平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点
?若存在,说明点 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.

如图,四棱锥 ,平面
,平面 ⊥平面
⊥平面 ,△
,△ 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且 .
.
(1)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为
为 上任意一点,试问点
上任意一点,试问点 在线段
在线段 上什么位置时,
上什么位置时, ⊥
⊥ ;
;
(3)若点 是
是 的中点,求
的中点,求 .
.
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是 的中点.
的中点.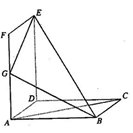
(1)求证: ;
;
(2)若直线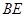 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分12分)如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=PC=2.E是PB的中点.
(1)求证:平面EAC⊥平面PBC;
(2)求二面角P—AC—E的余弦值;
(3)求直线PA与平面EAC所成角的正弦值.
(本小题满分12分)如图所示,正方形 和矩形
和矩形 所在平面相互垂直,
所在平面相互垂直, 是
是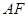 的中点.
的中点.
(1)求证: ;
;
(2)若直线 与平面
与平面 成45o角,求异面直线
成45o角,求异面直线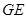 与
与 所成角的余弦值.
所成角的余弦值.
(本小题满分10分)直三棱柱ABC—A′B′C′中,AC=BC=AA′,∠ACB=90°,D、E分别为AB、BB′的中点.
(1)求证:
 ;
;
(2)求证: 平面
平面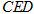 .
.