已知函数 .
.
(1)当 时,求函数
时,求函数 的单调增区间;
的单调增区间;
(2)当 时,求函数
时,求函数 在区间
在区间 上的最小值;
上的最小值;
(3)记函数 图象为曲线
图象为曲线 ,设点
,设点 ,
, 是曲线
是曲线 上不同的两点,点
上不同的两点,点 为线段
为线段 的中点,过点
的中点,过点 作
作 轴的垂线交曲线
轴的垂线交曲线 于点
于点 .试问:曲线
.试问:曲线 在点
在点 处的切线是否平行于直线
处的切线是否平行于直线 ?并说明理由.
?并说明理由.
如图,已知 ,
, ,
, ,
, 分别是椭圆
分别是椭圆 的四个顶点,△
的四个顶点,△ 是一个边长为2的等边三角形,其外接圆为圆
是一个边长为2的等边三角形,其外接圆为圆 .
.
(1)求椭圆 及圆
及圆 的方程;
的方程;
(2)若点 是圆
是圆 劣弧
劣弧 上一动点(点
上一动点(点 异于端点
异于端点 ,
, ),直线
),直线 分别交线段
分别交线段 ,椭圆
,椭圆 于点
于点 ,
, ,直线
,直线 与
与 交于点
交于点 .
.
(ⅰ)求 的最大值;
的最大值;
(ⅱ)试问:. .,
., 两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
两点的横坐标之和是否为定值?若是,求出该定值;若不是,说明理由.
各项均为正数的数列{an}中,设 ,
, ,且
,且 ,
, .
.
(1)设 ,证明数列{bn}是等比数列;
,证明数列{bn}是等比数列;
(2)设 ,求集合
,求集合 .
.
已知函数 在
在 时取得极小值.
时取得极小值.
(1)求实数 的值;
的值;
(2)是否存在区间 ,使得
,使得 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出 ,
, 的值;
的值;
若不存在,说明理由.
已知函数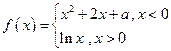 其中a是实数.设
其中a是实数.设 ,
, 为该函数图象上的两点,且
为该函数图象上的两点,且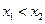 .
.
(1)指出函数f(x)的单调区间;
(2)若函数f(x)的图象在点A,B处的切线互相垂直,且 ,求
,求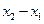 的最小值;
的最小值;
(3)若函数f(x)的图象在点A,B处的切线重合,求a的取值范围.
已知函数 .
.
(1)讨论f(x)在区间(0,1)上的单调性;
(2)当a∈[3,+∞)时,曲线 上总存在相异的两点
上总存在相异的两点 ,使得曲线
,使得曲线 在点P,Q处的切线互相平行,求证:
在点P,Q处的切线互相平行,求证: .
.
已知函数 .
.
(1)若直线 与
与 的反函数的图象相切,求实数k的值;
的反函数的图象相切,求实数k的值;
(2)设 ,讨论曲线
,讨论曲线 与曲线
与曲线 公共点的个数;
公共点的个数;
(3)设 ,比较
,比较 与
与 的大小,并说明理由.
的大小,并说明理由.
已知a,b是不相等的正数,在a,b之间分别插入m个正数a1,a2, ,am和正数b1,b2, ,
bm,使a,a1,a2, ,am,b是等差数列,a,b1,b2, ,bm,b是等比数列.
(1)若m=5, =
= ,求
,求 的值;
的值;
(2)若b=λa(λ∈N*,λ≥2),如果存在n (n∈N*,6≤n≤m)使得an-5=bn,求λ的最小值及此时m的值;
(3)求证:an>bn(n∈N*,n≤m).
已知函数 (
( )
)
(1)若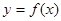 在点
在点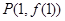 处的切线方程为
处的切线方程为 ,求
,求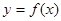 的解析式及单调递减区间;
的解析式及单调递减区间;
(2)若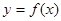 在
在 上存在极值点,求实数
上存在极值点,求实数 的取值范围.
的取值范围.
已知函数
(1)若方程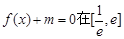 内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
内有两个不等的实根,求实数m的取值范围;(e为自然对数的底数)
(2)如果函数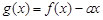 的图象与x轴交于两点
的图象与x轴交于两点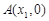 、
、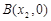 且
且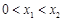 .求证:
.求证: (其中正常数
(其中正常数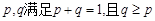 ).
).
已知椭圆C的两个焦点分别为 ,且点
,且点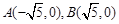 在椭圆C上,又
在椭圆C上,又 .
.
(1)求焦点F2的轨迹 的方程;
的方程;
(2)若直线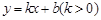 与曲线
与曲线 交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
交于M、N两点,以MN为直径的圆经过原点,求实数b的取值范围.
如图,已知四棱锥 的底面的菱形,
的底面的菱形, ,点
,点 是
是 边的中点,
边的中点, 交于点
交于点 ,
,

(1)求证: ;
;
(2)若 的大小;
的大小;
(3)在(2)的条件下,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
如图,已知椭圆 的左、右焦点分别
的左、右焦点分别
为 ,其上顶点为
,其上顶点为 已知
已知 是边长为
是边长为 的正三角形.
的正三角形.
(1)求椭圆 的方程;
的方程;
(2)过点 任作一动直线
任作一动直线 交椭圆
交椭圆 于
于 两点,记
两点,记 .若在线段
.若在线段 上取一点
上取一点 ,使得
,使得 ,当直线
,当直线 运动时,点
运动时,点 在某一定直线上运动,求出该定直线的方程.
在某一定直线上运动,求出该定直线的方程.