已知椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.
(1)求椭圆C的方程;
(2)设椭圆C的左右焦点分别为 ,
, ,过点
,过点 的直线
的直线 与椭圆C交于
与椭圆C交于 两点.
两点.
①当直线 的倾斜角为
的倾斜角为 时,求
时,求 的长;
的长;
②求 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线 的方程.
的方程.
如图,已知圆 ,经过椭圆
,经过椭圆 的右焦点F及上顶点B,过圆外一点
的右焦点F及上顶点B,过圆外一点 倾斜角为
倾斜角为 的直线
的直线 交椭圆于C,D两点,
交椭圆于C,D两点,
(1)求椭圆的方程;
(2)若右焦点F在以线段CD为直径的圆E的外部,求m的取值范围.
·大纲理)已知双曲线C: (a>0,b>0)的左、右焦点分别为
(a>0,b>0)的左、右焦点分别为 、
、 ,离心率为3,直线y=2与C的两个交点间的距离为
,离心率为3,直线y=2与C的两个交点间的距离为 .
.
(1)求a,b;
(2)设过 的直线l与C的左、右两支分别交于A、B两点,且
的直线l与C的左、右两支分别交于A、B两点,且 ,证明:
,证明: 、
、 、
、 成等比数列.
成等比数列.
已知椭圆 的离心率为
的离心率为 ,且经过点
,且经过点 ,圆
,圆 的直径为
的直径为 的长轴.如图,
的长轴.如图, 是椭圆短轴端点,动直线
是椭圆短轴端点,动直线 过点
过点 且与圆
且与圆 交于
交于 两点,
两点, 垂直于
垂直于 交椭圆于点
交椭圆于点 .
.

(1)求椭圆 的方程;
的方程;
(2)求 面积的最大值,并求此时直线
面积的最大值,并求此时直线 的方程.
的方程.
已知双曲线 的中心为原点
的中心为原点 ,左、右焦点分别为
,左、右焦点分别为 、
、 ,离心率为
,离心率为 ,点
,点 是直线
是直线 上任意一点,点
上任意一点,点 在双曲线
在双曲线 上,且满足
上,且满足 .
.
(1)求实数 的值;
的值;
(2)证明:直线 与直线
与直线 的斜率之积是定值;
的斜率之积是定值;
(3)若点 的纵坐标为
的纵坐标为 ,过点
,过点 作动直线
作动直线 与双曲线右支交于不同的两点
与双曲线右支交于不同的两点 、
、 ,在线段
,在线段 上去异于点
上去异于点 、
、 的点
的点 ,满足
,满足 ,证明点
,证明点 恒在一条定直线上.
恒在一条定直线上.
安徽理)(设椭圆 的焦点在
的焦点在 轴上
轴上
(1)若椭圆 的焦距为1,求椭圆
的焦距为1,求椭圆 的方程;
的方程;
(2)设 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点, 为椭圆
为椭圆 上第一象限内的点,直线
上第一象限内的点,直线 交
交 轴与点
轴与点 ,并且
,并且 ,证明:当
,证明:当 变化时,点
变化时,点 在某定直线上。
在某定直线上。
已知关于x的方程: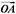 ·x2+
·x2+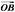 ·2x+
·2x+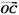 =0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
=0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
| A.点C在线段AB上 |
| B.点C在线段AB的延长线上且点B为线段AC的中点 |
| C.点C在线段AB的反向延长线上且点A为线段BC的中点 |
| D.以上情况均有可能 |
·广东理)设数列 的前
的前 项和为
项和为 .已知
.已知 ,
, ,
, .
.
(1) 求 的值;
的值;
(2) 求数列 的通项公式;
的通项公式;
(3) 证明:对一切正整数 ,有
,有 .
.
已知函数 ,其中
,其中 ,
, 是自然对数的底数.
是自然对数的底数.
(1)求函数 的零点;
的零点;
(2)若对任意 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知 ,且函数
,且函数 在R上是单调函数,探究函数
在R上是单调函数,探究函数 的单调性.
的单调性.
设[x]表示不超过x的最大整数(如[2]=2,[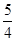 ]=1),对于给定的n
]=1),对于给定的n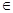 N*,定义
N*,定义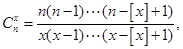 x
x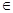
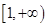 ,则当x
,则当x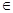
 时,函数
时,函数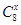 的值域是( )
的值域是( )
A.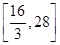 |
B.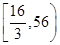 |
C.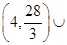 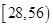 |
D.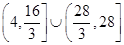 |
天津理)已知函数 .
.
(1) 求函数f(x)的单调区间;
(2) 证明: 对任意的t>0, 存在唯一的s, 使 .
.
(3) 设(2)中所确定的s关于t的函数为 , 证明: 当
, 证明: 当 时, 有
时, 有 .
.
上海理)给定常数 ,定义函数
,定义函数 ,数列
,数列 满足
满足 .
.
(1)若 ,求
,求 及
及 ;
;
(2)求证:对任意 ,;
,;
(3)是否存在 ,使得
,使得 成等差数列?若存在,求出所有这样的
成等差数列?若存在,求出所有这样的 ,若不存在,说明理由.
,若不存在,说明理由.
广东理)设函数 (其中
(其中 ).
).
(1) 当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2) 当 时,求函数
时,求函数 在
在 上的最大值
上的最大值 .
.
已知椭圆G: .过点(m,0)作圆
.过点(m,0)作圆 的切线l交椭圆G于A,B两点.
的切线l交椭圆G于A,B两点.
(1)求椭圆G的焦点坐标和离心率;
(2)将 表示为m的函数,并求
表示为m的函数,并求 的最大值.
的最大值.
已知点 ,圆C:
,圆C: 与椭圆E:
与椭圆E: 有一个公共点
有一个公共点 ,
, 分别是椭圆的左、右焦点,直线
分别是椭圆的左、右焦点,直线 与圆C相切.
与圆C相切.
(1)求m的值与椭圆E的方程;
(2)设Q为椭圆E上的一个动点,求 的取值范围.
的取值范围.