备战高频考点与最新模拟专题7平面向量
已知关于x的方程: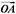 ·x2+
·x2+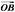 ·2x+
·2x+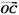 =0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
=0(x∈R),其中点C为直线AB上一点,O是直线AB外一点,则下列结论正确的是 ( )
| A.点C在线段AB上 |
| B.点C在线段AB的延长线上且点B为线段AC的中点 |
| C.点C在线段AB的反向延长线上且点A为线段BC的中点 |
| D.以上情况均有可能 |
已知向量a=(cosα,sinα),b=(cosβ,sinβ),c=(-1,0).
(1)求向量b+c的长度的最大值;
(2)设α= ,且a⊥(b+c),求cosβ的值.
,且a⊥(b+c),求cosβ的值.
(1)a,b是不共线的向量,若 =λ1a+b,
=λ1a+b, =a+λ2b(λ1,λ2∈R),则A,B,C三点共线的充要条件为( )
=a+λ2b(λ1,λ2∈R),则A,B,C三点共线的充要条件为( )
A.λ1=λ2=-1 B.λ1=λ2=1
C.λ1·λ2+1=0 D.λ1λ2-1=0
(2) 设A1,A2,A3,A4是平面直角坐标系中两两不同的四点,若 =λ
=λ (λ∈R),
(λ∈R), =μ
=μ (μ∈R),且
(μ∈R),且 +
+ =2,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,0)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
=2,则称A3,A4调和分割A1,A2,已知点C(c,0),D(d,0)(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是( )
A.C可能是线段AB的中点
B.D可能是线段AB的中点
C.C、D可能同时在线段AB上
D.C、D不可能同时在线段AB的延长线上
已知椭圆 +
+ =1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
=1(a>b>0)的左、右焦点分别为F1、F2,左顶点为A,若|F1F2|=2,椭圆的离心率为e=
(1)求椭圆的标准方程;
(2)若P是椭圆上的任意一点,求 的取值范围;
的取值范围;
(3)已知直线l:y=kx+m与椭圆相交于不同的两点M,N(均不是长轴的端点),AH⊥MN,垂足为H且 =
= ,求证:直线l恒过定点.
,求证:直线l恒过定点.
如图,四边形ABCD是半径为1的圆O的外切正方形, 是圆O的内接正三角形,当
是圆O的内接正三角形,当 绕着圆心O旋转时,
绕着圆心O旋转时, 的取值范围是( )
的取值范围是( )

A. |
B. |
C. |
D. |
如图,四边形 是边长为1的正方形,
是边长为1的正方形, ,点
,点 为
为 内(含边界)的动点,设
内(含边界)的动点,设 ,则
,则 的最大值等于( )
的最大值等于( )

A. |
B.1 | C. |
D. |
在平面直角坐标系中,菱形OABC的两个顶点为O(0,0),A(l,1),且 =1,则
=1,则 等于( )
等于( )
| A.-1 | B.1 | C. |
D. |
已知在△ABC中,AB=AC=4,BC=4 ,点P为边BC所在直线上的一个动点,则关于
,点P为边BC所在直线上的一个动点,则关于 ·(
·( +
+ )的值,下列选项正确的是( )
)的值,下列选项正确的是( )
| A.最大值为16 | B.为定值8 |
| C.最小值为4 | D.与P的位置有关 |
已知圆O的半径为1,PA,PB为该圆的两条切线,A,B为两切点,那么 的最小值等于.( )
的最小值等于.( )
A. |
B. |
C. |
D. |
若 (
( )是
)是 所在的平面内的点,且
所在的平面内的点,且 .
.
给出下列说法:① ;②
;② 的最小值一定是
的最小值一定是 ;
;
③点 、
、 在一条直线上.其中正确的个数是( )
在一条直线上.其中正确的个数是( )
| A.0个. | B.1个. | C.2个. | D.3个. |
如图,A是半径为5的圆O上的一个定点,单位向量 在A点处与圆O 相切,点P是圆O上的一个动点,且点P与点A不重合,则
在A点处与圆O 相切,点P是圆O上的一个动点,且点P与点A不重合,则 ·
· 的取值范围是 .
的取值范围是 . 
甲、乙两位同学参加2014年的自主招生考试,下火车后两人共同提起一个行李包(如图所示)。设他们所用的力分别为 ,行李包所受重力为
,行李包所受重力为 ,若
,若 ,则
,则 与
与 的夹角
的夹角 的大小为 .
的大小为 .
如图,已知四棱柱ABCD-A1B1C1D1的底面ABCD是矩形,AB=4,AA1=3,ÐBAA1=60°,E为棱C1D1的中点,则 .
.
已知向量 (
( 为常数且
为常数且 ),函数
),函数 在
在 上的最大值为
上的最大值为 .
.
(1)求实数 的值;
的值;
(2)把函数 的图象向右平移
的图象向右平移 个单位,可得函数
个单位,可得函数 的图象,若
的图象,若 在
在 上为增函数,求
上为增函数,求 取最大值时的单调增区间.
取最大值时的单调增区间.
 ,则|a+2b|=( )
,则|a+2b|=( )



 是
是 边
边 延长线上一点,记
延长线上一点,记 . 若关于
. 若关于 的方程
的方程 在
在 上恰有两解,则实数
上恰有两解,则实数 的取值范围是( )
的取值范围是( )
 或
或
 或
或 ,
,
 ,
,
 ,若
,若 为实数,
为实数, ,则
,则 的值为( )
的值为( )



 为单位向量,当
为单位向量,当 的夹角为
的夹角为 时,
时, 在
在 上的投影为( )
上的投影为( )



 中,
中, ,P为AB边上的点
,P为AB边上的点 ,若
,若 ,则
,则 的取值范围是( )
的取值范围是( )



 ,
, ,若
,若 ,则
,则 ( )
( ) 与
与 的夹角为
的夹角为 ,且
,且 ,若
,若 ,且,
,且, ,则实数
,则实数 的值为( )
的值为( )



 ,
, 满足
满足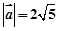 ,
, 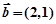 ,且
,且 ,设
,设 ∥
∥ ,若
,若
 ,则
,则 的值为 .
的值为 .
 ,
, 若
若 ,则
,则 _____________.
_____________. ,则
,则 .
. 与
与 的夹角为
的夹角为 ,
, ,
, 则
则 _______.
_______. 在
在 上的投影为 。
上的投影为 。 角
角 ,过
,过 作
作 ,且
,且 ,则
,则 .
. 、
、 的夹角为
的夹角为 ,且
,且 ,
, ,则向量
,则向量 的夹角等于 .
的夹角等于 . ,
, .
. ,
, ,且
,且 ,求
,求 ;
; ,求
,求 的取值范围.
的取值范围. 粤公网安备 44130202000953号
粤公网安备 44130202000953号