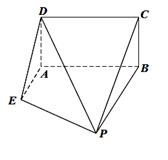
如图,已知矩形 所在平面垂直于直角梯形
所在平面垂直于直角梯形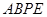 所在平面于直线
所在平面于直线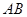 ,且
,且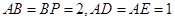 ,
,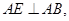 且
且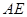 ∥
∥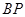 .
.
(Ⅰ)设点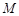 为棱
为棱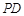 中点,求证:
中点,求证: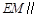 平面
平面 ;
;
(Ⅱ)线段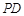 上是否存在一点
上是否存在一点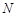 ,使得直线
,使得直线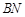 与平面
与平面 所成角的正弦值等于
所成角的正弦值等于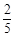 ?若存在,试确定点
?若存在,试确定点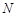 的位置;若不存在,请说明理由.
的位置;若不存在,请说明理由.
已知命题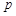 :函数
:函数 的图象恒过定点
的图象恒过定点 ;命题
;命题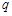 :若函数
:若函数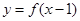 为偶函数,则函数
为偶函数,则函数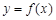 的图象关于直线
的图象关于直线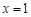 对称,则下列命题为真命题的是( )
对称,则下列命题为真命题的是( )
A. |
B.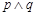 |
C.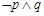 |
D. |
已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切. 是椭圆
是椭圆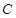 的右顶点与上顶点,直线
的右顶点与上顶点,直线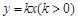 与椭圆相交于
与椭圆相交于 两点.
两点.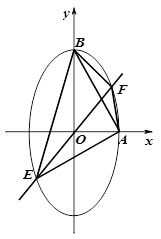
(Ⅰ)求椭圆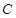 的方程;
的方程;
(Ⅱ)当四边形 面积取最大值时,求
面积取最大值时,求 的值.
的值.
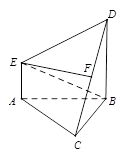
如图,在多面体 中,
中,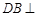 平面
平面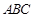 ,
,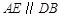 ,且
,且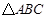 是边长为
是边长为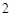 的等边三角形,
的等边三角形,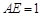 ,
,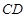 与平面
与平面 所成角的正弦值为
所成角的正弦值为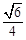 .
.
(Ⅰ)若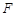 是线段
是线段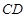 的中点,证明:
的中点,证明: 面
面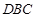 ;
;
(Ⅱ)求二面角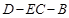 的平面角的余弦值.
的平面角的余弦值.