已知函数f(x)=loga(1﹣x)+loga(x+3)(0<a<1)
(1)求函数f(x)的定义域;
(2)求函数f(x)的零点;
(3)若函数f(x)的最小值为﹣4,求a的值.
关于函数f(x)=4sin(2x+ ),(x∈R)有下列命题:
),(x∈R)有下列命题:
①y=f(x)是以2π为最小正周期的周期函数;
②y=f(x)可改写为y=4cos(2x﹣ );
);
③y=f(x)的图象关于点(﹣ ,0)对称;
,0)对称;
④y=f(x)的图象关于直线x= 对称;
对称;
其中正确的序号为 .
已知函数f(x)=k(x﹣1)ex+x2.
(Ⅰ)当时k=﹣ ,求函数f(x)在点(1,1)处的切线方程;
,求函数f(x)在点(1,1)处的切线方程;
(Ⅱ)若在y轴的左侧,函数g(x)=x2+(k+2)x的图象恒在f(x)的导函数f′(x)图象的上方,求k的取值范围;
(Ⅲ)当k≤﹣l时,求函数f(x)在[k,1]上的最小值m.
已知P={x|x2﹣8x﹣20≤0},S={x|1﹣m≤x≤1+m}
(1)是否存在实数m,使x∈P是x∈S的充要条件,若存在,求出m的取值范围;
(2)是否存在实数m,使x∈P是x∈S的必要条件,若存在,求出m的取值范围.
已知公差不为零的等差数列{an},若a1=1,且a1,a2,a5成等比数列.
(1)求数列{an}的通项公式;
(2)设bn=2n,求数列{an+bn}的前n项和Sn.
学校从参加高二年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
| 分组 |
频数 |
频率 |
| [40,50) |
2 |
0.04 |
| [50,60) |
3 |
0.06 |
| [60,70) |
14 |
0.28 |
| [70,80) |
15 |
0.30 |
| [80,90) |
A |
B |
| [90,100] |
4 |
0.08 |
| 合计 |
C |
D |
(1)在给出的样本频率分布表中,求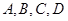 的值;
的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.
样本频率分布表如下: