正项数列{an}满足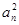 -(2n-1)an-2n=0.
-(2n-1)an-2n=0.
(1)求数列{an}的通项公式an.
(2)令bn= ,求数列{bn}的前n项和Tn.
,求数列{bn}的前n项和Tn.
如图,在平面直角坐标系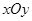 中,圆
中,圆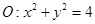 交
交 轴于点
轴于点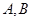 (点
(点 在
在 轴的负半轴上),点
轴的负半轴上),点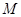 为圆
为圆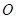 上一动点,
上一动点, 分别交直线
分别交直线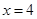 于
于 两点。
两点。
(1)求 两点纵坐标的乘积;
两点纵坐标的乘积;
(2)若点 的坐标为
的坐标为 ,连接
,连接 交圆
交圆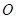 于另一点
于另一点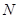 .
.
①试判断点 与以
与以 为直径的圆的位置关系,并说明理由;
为直径的圆的位置关系,并说明理由;
②记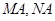 的斜率分别为
的斜率分别为 ,试探究
,试探究 是否为定值?若是,请求出该定值;若不是,请说明理由.
是否为定值?若是,请求出该定值;若不是,请说明理由.
某车间将10名技工平均分为甲,乙两组加工某种零件,在单位时间内每个技工加工零件若干,其中合格零件的个数如下表:
(1)分别求出甲,乙两组技工在单位时间内完成合格零件的平均数及方差,并由此分析两组技工的技术水平;
(2)质检部门从该车间甲,乙两组中各随机抽取1名技工,对其加工的零件进行检测,若两人完成合格零件个数之和超过12件,则称该车间“质量合格”,求该车间“质量合格”的概率.
选修4-4:坐标系与参数方程
在直角坐标系中,以原点为极点, 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ,过点
,过点 的直线
的直线 的参数方程为
的参数方程为 (
( 为参数),直线
为参数),直线 与曲线
与曲线 分别交于
分别交于 两点.
两点.
(1)写出曲线 的平面直角坐标方程和直线
的平面直角坐标方程和直线 的普通方程;
的普通方程;
(2)若 成等比数列,求实数
成等比数列,求实数 的值.
的值.