心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30,女20),给所有同学几何体和代数题各一题,让各位同学自由选择一道题进行解答,选题情况如下表(单位:人)
| |
几何题 |
代数题 |
总计 |
| 男同学 |
22 |
8 |
30 |
| 女同学 |
8 |
12 |
20 |
| 总计 |
30 |
20 |
50 |
(1)能否据此判断有97.5%的把握认为视觉和空间能力与性别有关?
(2)经过多次测试后,甲每次解答一道几何题所用的时间在5-7分钟,乙每次解答一道几何题所用的时间在6-8分钟,现甲,乙各解同一道几何题,求乙比甲先解答完的概率;
(3)现从选择做几何题的8名女生中任意抽取两人对她们的大题情况进行全程研究,记甲、乙两女生被抽到的人数为 ,求
,求 的分布列及数学期望
的分布列及数学期望 .
.
附表及公式:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |

如图,在四棱锥 中,底面
中,底面 是直角梯形,侧棱
是直角梯形,侧棱 底面
底面 ,
, 垂直于
垂直于 和
和 ,
, 是棱
是棱 的中点.
的中点.
(1)求证: 平面
平面 ;
;
(2)求平面 与平面
与平面 所成的二面角的余弦值;
所成的二面角的余弦值;
(3)设点 是直线
是直线 上的动点,
上的动点, 与平面
与平面 所成的角为
所成的角为 ,求
,求 的最大值.
的最大值.
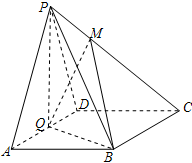
如图,在四棱锥 中,底面ABCD为菱形,
中,底面ABCD为菱形,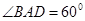 ,Q为AD的中点,
,Q为AD的中点, .
.
(1)求证: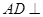 平面PQB;
平面PQB;
(2)点M在线段PC上,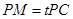 ,试确定t的值,使
,试确定t的值,使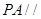 平面MQB.
平面MQB.
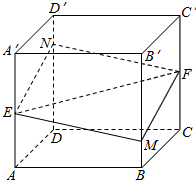
如图所示,正方体 的棱长为1,E、F分别是棱
的棱长为1,E、F分别是棱 的中点,过直线E、F的平面分别与棱
的中点,过直线E、F的平面分别与棱 、
、 交于M、N,设
交于M、N,设 ,
,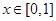 ,给出以下四种说法:
,给出以下四种说法:
(1)平面 平面
平面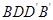 ;
;
(2)当且仅当 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
(3)四边形MENF周长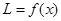 ,
,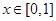 是单调函数;
是单调函数;
(4)四棱锥 的体积
的体积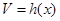 为常函数,以上说法中错误的为( )
为常函数,以上说法中错误的为( )
| A.(1)(4) | B.(2) | C.(3) | D.(3)(4) |
选修4-4:坐标系与参数方程
在直角坐标系 中,圆
中,圆 的参数方程为
的参数方程为 ,(
,( 为参数),以
为参数),以 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆 的极坐标方程;
的极坐标方程;
(2)直线 的极坐标方程是
的极坐标方程是 ,射线
,射线 与圆
与圆 的交点为
的交点为 ,与直线
,与直线 的交点为
的交点为 ,求线段
,求线段 的长.
的长.
设 三个内角
三个内角 所对的边分别为
所对的边分别为 ,已知
,已知 ,
, .
.
(1)求角 的大小;
的大小;
(2)如图,在 内取一点
内取一点 ,使得
,使得 ,过点
,过点 分别作直线
分别作直线 的垂线
的垂线 ,垂足分别是
,垂足分别是 ,设
,设 ,求
,求 的最大值及此时
的最大值及此时 的值.
的值.
已知圆 及抛物线
及抛物线 ,过圆心
,过圆心 作直线
作直线 ,此直线与两曲线有四个交点,自左向右顺次记为
,此直线与两曲线有四个交点,自左向右顺次记为 . 如果线段
. 如果线段 的长按此顺序构成一个等差数列,则直线
的长按此顺序构成一个等差数列,则直线 的方程为( )
的方程为( )
A. |
B. 或 或 |
C. |
D. 或 或 |