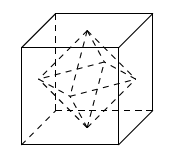
如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________
在平面直角坐标系 中,若双曲线 的右焦点 到一条渐近线的距离为 ,则其离心率的值是________
某兴趣小组有2名男生和3名女生,现从中任选2名学生去参加活动,则恰好选中2名女生的概率是________.
已知5位裁判给某运动员打出的分数的茎叶图如图所示,那么这5位裁判打出的分数的平均数为________.

如图,设椭圆
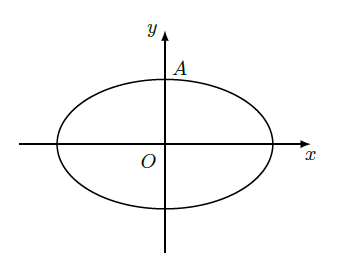
(1)求直线 被椭圆截得到的弦长(用a,k表示)
(2)若任意以点 为圆心的圆与椭圆至多有三个公共点,求椭圆的离心率的取值范围.
已知 ,函数 ,其中
(1)求使得等式 成立的x的取值范围
(2)(1)求 的最小值
(3)求 在 上的最大值
如图,在三棱台 中,已知平面 平面 , , , , ,
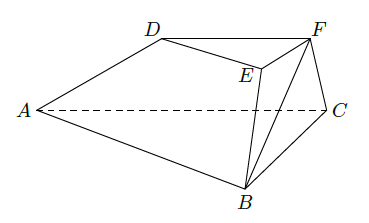
(1)求证: 平面 ;
(2)求二面角 的余弦值.