正三角形ABC的边长为2 ,将它沿高AD翻折,使点B与点C间的距离为
,将它沿高AD翻折,使点B与点C间的距离为 ,此时四面体ABCD的外接球的体积为。
,此时四面体ABCD的外接球的体积为。
如图,四棱锥P-ABCD中,底面ABCD为正方形,DA⊥面ABP,AB=1,PA=2,∠PAB=600,E为PA的中点,F为PC上不同于P、C的任意一点.
(1)求证:PC∥面EBD
(2)求异面直线AC与PB间的距离
(3)求三棱锥E-BDF的体积.
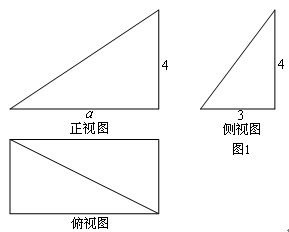
已知某几何体的三视图如图所示,若该几何体的体积为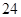 ,则正视图中
,则正视图中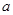 的值为()
的值为()
A. |
B.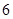 |
C.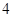 |
D.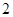 |
一平面截一球得到直径为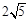 cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是()
cm的圆面,球心到这个平面的距离是2 cm,则该球的体积是()
| A.12 cm3 | B.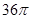 cm3 cm3 |
C. cm3 cm3 |
D.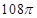 cm3 cm3 |
一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为 ,那么这个三棱柱的体积是_____________.
,那么这个三棱柱的体积是_____________.
已知正方形ABCD,AB=2,若将 沿正方形的对角线BD所在的直线进行翻折,则在翻折的过程中,四面体
沿正方形的对角线BD所在的直线进行翻折,则在翻折的过程中,四面体 的体积的最大值是____.
的体积的最大值是____.
已知圆锥的底面半径为R,高为3R,在它的所有内接圆柱中,全面积的最大值是( )
| A.22πR2 | B. πR2 πR2 |
C. πR2 πR2 |
D. πR2 πR2 |
如图,在三棱锥 中,
中, ,
, ,平面
,平面 平面
平面 ,
, 为
为 中点,点
中点,点 分别为线段
分别为线段 上的动点(不含端点),且
上的动点(不含端点),且 ,则三棱锥
,则三棱锥 体积的最大值为________.
体积的最大值为________.
在三棱锥P-ABC中, .
.
(1)求证:平面 平面
平面 ;
;
(2)求BC与平面PAB所成角的正弦值;
(3)在棱BC上是否存在点Q使得AQ与PC成 的角?若存在,求BQ的长;若不存在,请说明理由.
的角?若存在,求BQ的长;若不存在,请说明理由.
已知一个三棱柱,其底面是正三角形,且侧棱与底面垂直,一个体积为 的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
的球体与棱柱的所有面均相切,那么这个三棱柱的表面积是( )
A. |
B. |
C. |
D. |
设△ABC的三边长分别为a、b、c,△ABC的面积为S,内切圆半径为r,则r= ;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
;类比这个结论可知:四面体S-ABC的四个面的面积分别为S1、S2、S3、S4,内切球的半径为r,四面体S-ABC的体积为V,则r=( )
A. |
B. |
C. |
D. |
如图,在四面体
中,
平面
,
.
是
的中点,
是
的中点,点
在线段
上,且
.
(1)证明:
平面
;
(2)若二面角
的大小为60°,求
的大小.
设A、B、C、D是半径为2的球面上的四点,且满足 ,
, 的最大值是_______ .
的最大值是_______ .
已知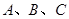 三点在球心为
三点在球心为 的球面上,
的球面上,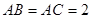 ,
, ,球心
,球心 到平面
到平面 的距离为
的距离为 ,则球
,则球 的表面积为 _ ______ .
的表面积为 _ ______ .