高考数学总复习考点引领+技巧点拨第九章第11课时练习卷
以双曲线 =1的中心为顶点,且以该双曲线的右焦点为焦点的拋物线方程是__________.
=1的中心为顶点,且以该双曲线的右焦点为焦点的拋物线方程是__________.
已知双曲线x2- =1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则
=1的左顶点为A1,右焦点为F2,P为双曲线右支上一点,则 的最小值为________.
的最小值为________.
已知椭圆C: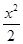 +y2=1的两焦点为F1,F2,点P(x0,y0)满足
+y2=1的两焦点为F1,F2,点P(x0,y0)满足 +
+ ≤1,则PF1+PF2的取值范围为________.
≤1,则PF1+PF2的取值范围为________.
如图,椭圆C: =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
(1)求椭圆C的方程;
(2)求△ABP面积取最大值时直线l的方程.
如图,在平面直角坐标系xOy中,椭圆的中心在原点O,右焦点F在x轴上,椭圆与y轴交于A、B两点,其右准线l与x轴交于T点,直线BF交椭圆于C点,P为椭圆上弧AC上的一点.
(1)求证:A、C、T三点共线;
(2)如果 =3
=3 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.
如图,椭圆C0: =1(a>b>0,a、b为常数),动圆C1:x2+y2=
=1(a>b>0,a、b为常数),动圆C1:x2+y2= ,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
,b<t1<a.点A1、A2分别为C0的左、右顶点,C1与C0相交于A、B、C、D四点.
(1)求直线AA1与直线A2B交点M的轨迹方程;
(2)设动圆C2:x2+y2= 与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明:
与C0相交于A′,B′,C′,D′四点,其中b<t2<a,t1≠t2.若矩形ABCD与矩形A′B′C′D′的面积相等,证明: 为定值.
为定值.
在平面直角坐标系xOy中,椭圆C: =1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
=1(a>b>0)的右焦点为F(4m,0)(m>0,m为常数),离心率等于0.8,过焦点F、倾斜角为θ的直线l交椭圆C于M、N两点.
(1)求椭圆C的标准方程;
(2)若θ=90°, ,求实数m;
,求实数m;
(3)试问 的值是否与θ的大小无关,并证明你的结论.
的值是否与θ的大小无关,并证明你的结论.
在平面直角坐标系xOy中,已知圆C1:(x+3)2+(y-1)2=4和圆C2:(x-4)2+(y-5)2=4.
(1)若直线l过点A(4,0),且被圆C1截得的弦长为2 ,求直线l的方程;
,求直线l的方程;
(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线l1和l2,它们分别与圆C1和圆C2相交,且直线l1被圆C1截得的弦长与直线l2被圆C2截得的弦长相等,试求所有满足条件的点P的坐标.
已知椭圆 +y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
+y2=1的左顶点为A,过A作两条互相垂直的弦AM、AN交椭圆于M、N两点.
(1)当直线AM的斜率为1时,求点M的坐标;
(2)当直线AM的斜率变化时,直线MN是否过x轴上的一定点?若过定点,请给出证明,并求出该定点;若不过定点,请说明理由.
如图,已知梯形ABCD中|AB|=2|CD|,点E满足 =λ
=λ ,双曲线过C、D、E三点,且以A、B为焦点.当
,双曲线过C、D、E三点,且以A、B为焦点.当 ≤λ≤
≤λ≤ 时,求双曲线离心率e的取值范围.
时,求双曲线离心率e的取值范围.
在平面直角坐标系xOy中,已知定点A(-4,0)、B(4,0),动点P与A、B连线的斜率之积为- .
.
(1)求点P的轨迹方程;
(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上,且在y轴右侧,圆M被y轴截得的弦长为 r.
r.
(ⅰ)求圆M的方程;
(ⅱ)当r变化时,是否存在定直线l与动圆M均相切?如果存在,求出定直线l的方程;如果不存在,说明理由.
如图,椭圆E: =1(a>b>0)的左焦点为F1,右焦点为F2,离心率e=
=1(a>b>0)的左焦点为F1,右焦点为F2,离心率e= .过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
.过F1的直线交椭圆于A、B两点,且△ABF2的周长为8.
(1)求椭圆E的方程;
(2)设动直线l:y=kx+m与椭圆E有且只有一个公共点P,且与直线x=4相交于点Q.试探究:在坐标平面内是否存在定点M,使得以PQ为直径的圆恒过点M?若存在,求出点M的坐标;若不存在,说明理由.
已知抛物线y2=2px(p≠0)上存在关于直线x+y=1对称的相异两点,则实数p的取值范围为________.
已知抛物线y2=2px(p≠0)及定点A(a,b),B(-a,0),ab≠0,b2≠2pa,M是抛物线上的点.设直线AM、BM与抛物线的另一个交点分别为M1、M2,当M变动时,直线M1M2恒过一个定点,此定点坐标为________.
在平面直角坐标系xOy中,抛物线C的顶点在原点,焦点F的坐标为(1,0).
(1)求抛物线C的标准方程;
(2)设M、N是抛物线C的准线上的两个动点,且它们的纵坐标之积为-4,直线MO、NO与抛物线的交点分别为点A、B,求证:动直线AB恒过一个定点.
已知椭圆E: +y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
+y2=1(a>1)的上顶点为M(0,1),两条过M的动弦MA、MB满足MA⊥MB.
(1)当坐标原点到椭圆E的准线距离最短时,求椭圆E的方程;
(2)若Rt△MAB面积的最大值为 ,求a;
,求a;
(3)对于给定的实数a(a>1),动直线AB是否经过一定点?如果经过,求出定点坐标(用a表示);反之,说明理由.
设A1、A2与B分别是椭圆E: =1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
=1(a>b>0)的左、右顶点与上顶点,直线A2B与圆C:x2+y2=1相切.
(1)求证: =1;
=1;
(2)P是椭圆E上异于A1、A2的一点,若直线PA1、PA2的斜率之积为- ,求椭圆E的方程;
,求椭圆E的方程;
(3)直线l与椭圆E交于M、N两点,且 ·
· =0,试判断直线l与圆C的位置关系,并说明理由.
=0,试判断直线l与圆C的位置关系,并说明理由.
已知曲线C上动点P(x,y)到定点F1( ,0)与定直线l1∶x=
,0)与定直线l1∶x= 的距离之比为常数
的距离之比为常数 .
.
(1)求曲线C的轨迹方程;
(2)以曲线C的左顶点T为圆心作圆T:(x+2)2+y2=r2(r>0),设圆T与曲线C交于点M与点N,求 ·
· 的最小值,并求此时圆T的方程.
的最小值,并求此时圆T的方程.
已知抛物线x2=4y的焦点为F,过焦点F且不平行于x轴的动直线交抛物线于A、B两点,抛物线在A、B两点处的切线交于点M.
(1)求证:A、M、B三点的横坐标成等差数列;
(2)设直线MF交该抛物线于C、D两点,求四边形ACBD面积的最小值.
已知椭圆C: =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,一条准线方程为x=
,一条准线方程为x=
(1)求椭圆C的方程;
(2)设G、H为椭圆C上的两个动点,O为坐标原点,且OG⊥OH.
①当直线OG的倾斜角为60°时,求△GOH的面积;
②是否存在以原点O为圆心的定圆,使得该定圆始终与直线GH相切?若存在,请求出该定圆方程;若不存在,请说明理由.
已知椭圆C的方程为 =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当 =λ
=λ ,求λ的最大值.
,求λ的最大值.
 =1的右焦点重合,则p=________.
=1的右焦点重合,则p=________.
 =λ
=λ ,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由.
,直线OP与QA交于点M,问:是否存在点P,使得△PQA和△PAM的面积满足S△PQA=2S△PAM?若存在,求出点P的坐标;若不存在,说明理由. 粤公网安备 44130202000953号
粤公网安备 44130202000953号