已知椭圆C：
＝1(a>b>0)的离心率e＝
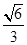，一条准线方程为x＝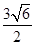
(1)求椭圆C的方程；
(2)设G、H为椭圆C上的两个动点，O为坐标原点，且OG⊥OH.
①当直线OG的倾斜角为60°时，求△GOH的面积；
②是否存在以原点O为圆心的定圆，使得该定圆始终与直线GH相切？若存在，请求出该定圆方程；若不存在，请说明理由．
相关试题
中，
平面
.
平面
；
，
为
中点，求三棱锥
的体积.
中，侧棱垂直底面，
，
，
是棱
的中点。
⊥平面
，求几何体
的体积。
．
的值；
，求
的值
中，
，点
在
边上，且
的长
推荐套卷
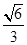已知椭圆C：＝1(a>b>0)的离心率e＝，一条准线方程为x＝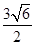
(1)求椭圆C的方程；
(2)设G、H为椭圆C上的两个动点，O为坐标原点，且OG⊥OH.
①当直线OG的倾斜角为60°时，求△GOH的面积；
②是否存在以原点O为圆心的定圆，使得该定圆始终与直线GH相切？若存在，请求出该定圆方程；若不存在，请说明理由．
粤公网安备 44130202000953号