甲、乙二射击运动员分别对一目标射击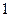
次，甲射中的概率为
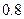，乙射中的概率为
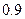，求：
（1）
人都射中目标的概率；
（2）人中恰有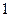人射中目标的概率；
（3）人至少有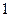人射中目标的概率；
（4）人至多有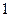人射中目标的概率？
相关试题
;
的直线方程；
中，
，点
分别在
上，且
，现将梯形
折起，使平面
与平面
垂直(如图②)．
平面
；
时，求二面角
的大小．
中，
，点
是
的中点.
；
平面
；
与
所成角的余弦值.
推荐套卷
甲、乙二射击运动员分别对一目标射击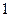次，甲射中的概率为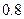，乙射中的概率为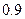，求：
（1）人都射中目标的概率；
（2）人中恰有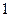人射中目标的概率；
（3）人至少有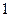人射中目标的概率；
（4）人至多有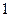人射中目标的概率？
粤公网安备 44130202000953号