已知椭圆C的方程为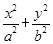 =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当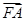 =λ
=λ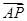 ,求λ的最大值.
,求λ的最大值.
相关知识点
推荐套卷
已知椭圆C的方程为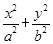 =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
(1)当l1与l2夹角为60°,双曲线的焦距为4时,求椭圆C的方程;
(2)当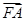 =λ
=λ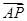 ,求λ的最大值.
,求λ的最大值.