已知曲线C上动点P(x，y)到定点F1(
，0)与定直线l1∶x＝
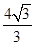的距离之比为常数
.
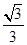(1)求曲线C的轨迹方程；
(2)以曲线C的左顶点T为圆心作圆T：(x＋2)2＋y2＝r2(r>0)，设圆T与曲线C交于点M与点N，求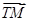
·
的最小值，并求此时圆T的方程．
（
），
，当
取何值时，（1）
；（2）
分别取什么值时，复数
是（1）实数（2）虚数（3）纯虚数。
的方程
有实根，求实数
的取值。
是纯虚数；推荐套卷
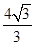已知曲线C上动点P(x，y)到定点F1(，0)与定直线l1∶x＝的距离之比为常数.
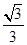(1)求曲线C的轨迹方程；
(2)以曲线C的左顶点T为圆心作圆T：(x＋2)2＋y2＝r2(r>0)，设圆T与曲线C交于点M与点N，求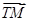·的最小值，并求此时圆T的方程．
粤公网安备 44130202000953号