在平面直角坐标系xOy中，已知定点A(－4，0)、B(4，0)，动点P与A、B连线的斜率之积为－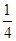
.
(1)求点P的轨迹方程；
(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为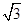
r.
(ⅰ)求圆M的方程；
(ⅱ)当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．
在定义域
上是减函数，且
，则
的 取值范围；
是偶函数，它在
上是减函数，若
，求
，
,
的单调性，并证明；
和
的值
时，求
的值
.
的值；（2）计算：
.
，
；（2）求
；推荐套卷
在平面直角坐标系xOy中，已知定点A(－4，0)、B(4，0)，动点P与A、B连线的斜率之积为－.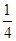
(1)求点P的轨迹方程；
(2)设点P的轨迹与y轴负半轴交于点C.半径为r的圆M的圆心M在线段AC的垂直平分线上，且在y轴右侧，圆M被y轴截得的弦长为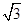r.
(ⅰ)求圆M的方程；
(ⅱ)当r变化时，是否存在定直线l与动圆M均相切？如果存在，求出定直线l的方程；如果不存在，说明理由．
粤公网安备 44130202000953号