如图,在平面直角坐标系xOy中,椭圆的中心在原点O,右焦点F在x轴上,椭圆与y轴交于A、B两点,其右准线l与x轴交于T点,直线BF交椭圆于C点,P为椭圆上弧AC上的一点.
(1)求证:A、C、T三点共线;
(2)如果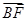 =3
=3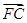 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.
推荐套卷
如图,在平面直角坐标系xOy中,椭圆的中心在原点O,右焦点F在x轴上,椭圆与y轴交于A、B两点,其右准线l与x轴交于T点,直线BF交椭圆于C点,P为椭圆上弧AC上的一点.
(1)求证:A、C、T三点共线;
(2)如果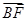 =3
=3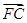 ,四边形APCB的面积最大值为
,四边形APCB的面积最大值为 ,求此时椭圆的方程和P点坐标.
,求此时椭圆的方程和P点坐标.