2007年全国统一高考理科数学试卷(广东卷)
若函数 ,则 是()
| A. | 最小正周期为 的奇函数; | B. | 最小正周期为 的奇函数; |
| C. | 最小正周期为 的偶函数; | D. | 最小正周期为 的偶函数; |
客车从甲地以60 的速度行驶1小时到达乙地,在乙地停留了半小时,然后以80 的速度行驶1小时到达丙地.下列描述客车从甲地出发,经过乙地,最后到达丙地所经过的路程 与时间 之间的关系图象中,正确的是( )
A.  B.
B. 
C.  D.
D. 
图1是某县参加2007年高考的学生身高条形统计图,从左到右的各条形图表示学生人数依次记为
(如
表示身高(单位:
)在
内的人数].图2是统计图1中身高在一定范围内学生人数的一个算法流程图.现要统计身高在
(含
,不含
)的学生人数,那么在流程图中的判断框内应填写的条件是( )


| A. | B. | C. | D. |
如图是某汽车维修公司的维修点分布图,公司在年初分配给 、 、 、 四个维修点的某种配件各 件,在使用前发现需将 、 、 、 四个维修点的这批配件分别调整为 、 、 、 件,但调整只能在相邻维修点之间进行,那么完成上述调整,最少的调动件次( 个配件从一个维修点调整到相邻维修点的调动件次为 )为( )

| A. | B. | C. | D. |
设
是至少含有两个元素的集合.在
上定义了一个二元运算"*"(即对任意的
,对于有序元素对
,在
中有唯一确定的元素
与之对应)。若对于任意的
,有
,则对任意的
,下列等式中不能成立的是
| A. |
|
B. |
|
| C. |
|
D. |
|
甲、乙两个袋子中均装有红、白两种颜色的小球,这些小球除颜色外完全相同,其中甲袋装有4个红球、2个白球,乙袋装有1个红球、5个白球。现分别从甲、乙两袋中各随机抽取一个球,则取出的两球是红球的概率为(答案用分数表示)
如果一个凸多面体是 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条,这些直线中共有 对异面直线,则 ; = (答案用数字或 的解析式表示)

在平面直角坐标系 中,直线l的参数方程为 (参数 ),圆 的参数方程为 (参数 ),则圆 的圆心坐标为,圆心到直线 的距离为.
如图所示,圆 的直径 , 为圆周上一点, .过 作圆的切线 ,过 作 的垂线 分别与直线 、圆交于点 、 ,则∠ = ,线段 的长为 。

已知 的三个顶点的直角坐标分别为 、 、
(1)若
,求
的值;
(2)若
为钝角,求
的取值范围;
下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据
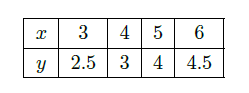
(1) 请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出
关于
的线性回归方程
;
(3)已知该厂技术改造前
吨甲产品能耗为
吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据:
)
在直角坐标系
中,已知圆心在第二象限、半径为
的圆
与直线
相切于坐标原点
.椭圆
与圆
的一个交点到椭圆两焦点的距离之和为10.
(1)求圆
的方程;
(2)试探究圆
上是否存在异于原点的点
,使
到椭圆的右焦点
的距离等于线段
的长,若存在求出
的坐标;若不存在,请说明理由.
如图所示,等腰三角形
的底边
,高
.点
是线段
上异于
的动点.点
在
边上,且
.现沿
将
折起到
的位置,使
.
记
表示四棱锥
的体积。
(1)求
的表达式;
(2)当
为何值时,
取得最大值?
(3)当
取得最大值时,求异面直线
与
所成角的余弦值。

 粤公网安备 44130202000953号
粤公网安备 44130202000953号