如图所示,等腰三角形
的底边
,高
.点
是线段
上异于
的动点.点
在
边上,且
.现沿
将
折起到
的位置,使
.
记
表示四棱锥
的体积。
(1)求
的表达式;
(2)当
为何值时,
取得最大值?
(3)当
取得最大值时,求异面直线
与
所成角的余弦值。
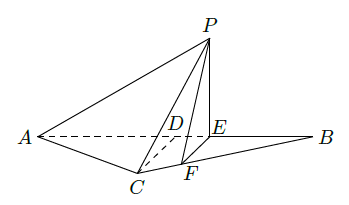
相关知识点
推荐套卷
如图所示,等腰三角形
的底边
,高
.点
是线段
上异于
的动点.点
在
边上,且
.现沿
将
折起到
的位置,使
.
记
表示四棱锥
的体积。
(1)求
的表达式;
(2)当
为何值时,
取得最大值?
(3)当
取得最大值时,求异面直线
与
所成角的余弦值。
