下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量
(吨)与相应的生产能耗
(吨标准煤)的几组对照数据

(1) 请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出
关于
的线性回归方程
;
(3)已知该厂技术改造前
吨甲产品能耗为
吨标准煤.试根据(2)求出的线性回归方程,预测生产
吨甲产品的生产能耗比技术改造前降低多少吨标准煤?
(参考数据:
)
相关知识点
推荐套卷
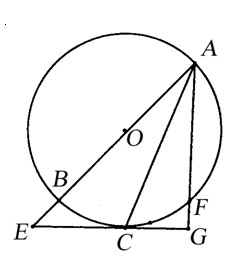
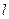 与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.
与圆O相切于C,交AB于E,且与AF垂直,垂足为G,连接AC.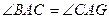

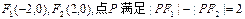 ,记点P的轨迹为E.
,记点P的轨迹为E.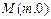 ,使
,使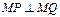 恒成立,求实数m的值.
恒成立,求实数m的值. 1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标.
1,y1),C(x2,y2)满足条件|F2A|,|F2B|,|F2C|成等差数列.(1)求该椭圆的方程;(2)求弦AC中点的横坐标. 且圆心在直线
且圆心在直线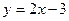 上的圆的方程
上的圆的方程 粤公网安备 44130202000953号
粤公网安备 44130202000953号