初中数学游戏公平性试题

小伟和小梅两位同学玩掷骰子的游戏，两人各掷一次均匀的骰子．以掷出的点数之差的绝对值判断输赢．若所得数值等于0，1，2，则小伟胜；若所得数值等于3，4，5，则小梅胜．

（1）请利用表格分别求出小伟、小梅获胜的概率；

（2）判断上述游戏是否公平．如果公平，请说明理由；如果不公平，请利用表格修改游戏规则，以确保游戏的公平性．

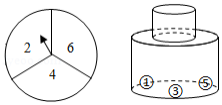
有一个可自由转动的转盘，被分成了三个大小相同的扇形，分别标有数字2，4，6；另有一个不透明的瓶子，装有分别标有数字1，3，5的三个完全相同的小球．小杰先转动一次转盘，停止后记下指针指向的数字（若指针指在分界线上则重转），小玉再从瓶子中随机取出一个小球，记下小球上的数字．

（1）请用列表或画树状图的方法（选其中一种）表示出所有可能出现的结果；

（2）若得到的两数字之和是3的倍数，则小杰贏；若得到的两数字之和是7的倍数，则小玉赢，此游戏公平吗？为什么？

小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果两次是一正一反，则我赢．”小红赢的概率是　　，据此判断该游戏　　（填“公平”或“不公平” $)$．

在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球，把它们充分搅匀．

（1）“从中任意抽取1个球不是红球就是白球”是　　事件，“从中任意抽取1个球是黑球”是　　事件；

（2）从中任意抽取1个球恰好是红球的概率是　　；

（3）学校决定在甲、乙两名同学中选取一名作为学生代表发言，制定如下规则：从盒子中任取两个球，若两球同色，则选甲；若两球异色，则选乙．你认为这个规则公平吗？请用列表法或画树状图法加以说明．

小明和小亮计划暑期结伴参加志愿者活动．小明想参加敬老服务活动，小亮想参加文明礼仪宣传活动．他们想通过做游戏来决定参加哪个活动，于是小明设计了一个游戏，游戏规则是：在三张完全相同的卡片上分别标记4、5、6三个数字，一人先从三张卡片中随机抽出一张，记下数字后放回，另一人再从中随机抽出一张，记下数字，若抽出的两张卡片标记的数字之和为偶数，则按照小明的想法参加敬老服务活动，若抽出的两张卡片标记的数字之和为奇数，则按照小亮的想法参加文明礼仪宣传活动．你认为这个游戏公平吗？请说明理由．

小华和小军做摸球游戏： $A$袋装有编号为1，2，3的三个小球， $B$袋装有编号为4，5，6的三个小球，两袋中的所有小球除编号外都相同．从两个袋子中分别随机摸出一个小球，若 $B$袋摸出小球的编号与 $A$袋摸出小球的编号之差为偶数，则小华胜，否则小军胜．这个游戏对双方公平吗？请说明理由．

如图是一个转盘，转盘被平均分成4等份，即被分成4个大小相等的扇形，4个扇形分别标有数字1、2、3、4，指针的位置固定，转动转盘后任其自由停止，每次指针落在每一扇形的机会均等（若指针恰好落在分界线上则重转）．

（1）图中标有“1”的扇形至少绕圆心旋转　　度能与标有“4”的扇形的起始位置重合；

（2）现有一本故事书，姐妹俩商定通过转盘游戏定输赢（赢的一方先看）．游戏规则是：姐妹俩各转动一次转盘，两次转动后，若指针所指扇形上的数字之积为偶数，则姐姐赢；若指针所指扇形上的数字之积为奇数，则妹妹赢．这个游戏规则对双方公平吗？请利用树状图或列表法说明理由．

甲、乙两人进行摸牌游戏．现有三张形状大小完全相同的牌，正面分别标有数字2，3，5．将三张牌背面朝上，洗匀后放在桌子上．

（1）甲从中随机抽取一张牌，记录数字后放回洗匀，乙再随机抽取一张．请用列表法或画树状图的方法，求两人抽取相同数字的概率；

（2）按照（1）中的抽法，若两人抽取的数字和为2的倍数，则甲获胜；若抽取的数字和为5的倍数，则乙获胜．这个游戏公平吗？请用概率的知识加以解释．

如图，有四张背面完全相同的纸牌 $A$、 $B$、 $C$、 $D$，其正面分别画有四个不同的几何图形，将这四张纸牌背面朝上洗匀．

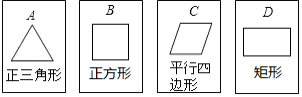
（1）从中随机摸出一张，求摸出的牌面图形是中心对称图形的概率；

（2）小明和小亮约定做一个游戏，其规则为：先由小明随机摸出一张纸牌，不放回，再由小亮从剩下的纸牌中随机摸出一张，若摸出的两张牌面图形都是轴对称图形小明获胜，否则小亮获胜，这个游戏公平吗？请用列表法（或树状图）说明理由（纸牌用 $A$、 $B$、 $C$、 $D$表示）．

一个盒子里有标号分别为1，2，3，4，5，6的六个小球，这些小球除标号数字外都相同．

（1）从盒中随机摸出一个小球，求摸到标号数字为奇数的小球的概率；

（2）甲、乙两人用这六个小球玩摸球游戏，规则是：甲从盒中随机摸出一个小球，记下标号数字后放回盒里，充分摇匀后，乙再从盒中随机摸出一个小球，并记下标号数字．若两次摸到小球的标号数字同为奇数或同为偶数，则判甲赢；若两次摸到小球的标号数字为一奇一偶，则判乙赢．请用列表法或画树状图的方法说明这个游戏对甲、乙两人是否公平．

小明和小亮用下面两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形．转动两个转盘各一次，若两次数字之积大于2，则小明胜，否则小亮胜．这个游戏对双方公平吗？请说明理由．

一只不透明的袋子中装有3个球，球上分别标有数字0，1，2，这些球除了数字外其余都相同，甲、乙两人玩摸球游戏，规则如下：先由甲随机摸出一个球（不放回），再由乙随机摸出一个球，两人摸出的球所标的数字之和为偶数时则甲胜，和为奇数时则乙胜．

（1）用画树状图或列表的方法列出所有可能的结果；

（2）这样的游戏规则是否公平？请说明理由．

如图所示，甲、乙两人在玩转盘游戏时，分别把转盘 $A$， $B$分成3等份和4等份，并在每一份内标上数字．游戏规则：同时转动两个转盘，当转盘停止后，指针所在区域的数字之积为奇数时，甲获胜；当数字之积为偶数时，乙获胜．如果指针恰好在分割线上时，则需重新转动转盘．

（1）利用画树状图或列表的方法，求甲获胜的概率．

（2）这个游戏规则对甲、乙双方公平吗？若公平，请说明理由；若不公平，请你在转盘 $A$上只修改一个数字使游戏公平（不需要说明理由）．

“端午节”是我国流传了上千年的传统节日，全国各地举行了丰富多彩的纪念活动．为了继承传统，减缓学生考前的心理压力，某班学生组织了一次拔河比赛，裁判员让两队队长用“石头、剪刀、布”的手势方式选择场地位置，规则是：石头胜剪刀，剪刀胜布，布胜石头，手势相同则再决胜负．

（1）用列表或画树状图法，列出甲、乙两队手势可能出现的情况；

（2）裁判员的这种做法对甲、乙双方公平吗？请说明理由．

由于只有1张市运动会开幕式的门票，小王和小张都想去，两人商量采取转转盘（如图，转盘盘面被分为面积相等，且标有数字1，2，3，4的4个扇形区域）的游戏方式决定谁胜谁去观看．规则如下：两人各转动转盘一次，当转盘指针停止，如两次指针对应盘面数字都是奇数，则小王胜；如两次指针对应盘面数字都是偶数，则小张胜；如两次指针对应盘面数字是一奇一偶，视为平局．若为平局，继续上述游戏，直至分出胜负．

如果小王和小张按上述规则各转动转盘一次，则

（1）小王转动转盘，当转盘指针停止，对应盘面数字为奇数的概率是多少？

（2）该游戏是否公平？请用列表或画树状图的方法说明理由．