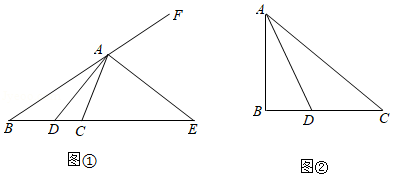
已知,如图①,若 是 中 的内角平分线,通过证明可得 ,同理,若 是 中 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:
如图②,在 中, , , 是 的内角平分线,则 的 边上的中线长 的取值范围是 .
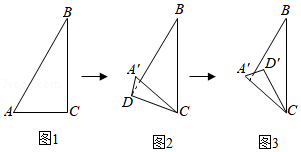
小华用一张直角三角形纸片玩折纸游戏,如图1,在 中, , , .第一步,在 边上找一点 ,将纸片沿 折叠,点 落在 处,如图2;第二步,将纸片沿 折叠,点 落在 处,如图3.当点 恰好落在原直角三角形纸片的边上时,线段 的长为 .
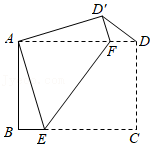
如图,在矩形 中, , ,将此矩形折叠,使点 与点 重合,点 落在点 处,折痕为 ,则 的长为 , 的长为 .
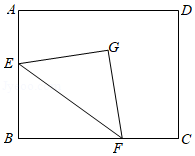
如图, 、 分别是正方形 的边 、 上的动点,满足 ,连接 、 ,相交于点 ,连接 ,若正方形的边长为2.则线段 的最小值为 .

在综合实践课上,老师要求同学用正方形纸片剪出正三角形且正三角形的顶点都在正方形边上.小红利用两张边长为2的正方形纸片,按要求剪出了一个面积最大的正三角形和一个面积最小的正三角形.则这两个正三角形的边长分别是 .
如图,在正六边形 中,连接对角线 , , , , , 与 交于点 , 与 交于点为 , 与 交于点 ,分别延长 , 于点 ,设 .有以下结论:
①
②
③ 的重心、内心及外心均是点
④四边形 绕点 逆时针旋转 与四边形 重合
则所有正确结论的序号是 .

如图,一次函数 与反比例函数 的图象交于 , 两点,点 在以 为圆心,半径为1的 上, 是 的中点,已知 长的最大值为 ,则 的值是 .

如图.在边长为6的正方形 中,点 , 分别在 , 上, 且 , ,垂足为 , 是对角线 的中点,连接 、则 的长为 .

如图,在矩形 中, , ,点 , 分别是边 , 上的动点,点 不与 , 重合,且 , 是五边形 内满足 且 的点.现给出以下结论:
① 与 一定互补;
②点 到边 , 的距离一定相等;
③点 到边 , 的距离可能相等;
④点 到边 的距离的最大值为 .
其中正确的是 .(写出所有正确结论的序号)
某企业有 , 两条加工相同原材料的生产线.在一天内, 生产线共加工 吨原材料,加工时间为 小时;在一天内, 生产线共加工 吨原材料,加工时间为 小时.第一天,该企业将5吨原材料分配到 , 两条生产线,两条生产线都在一天内完成了加工,且加工时间相同,则分配到 生产线的吨数与分配到 生产线的吨数的比为 .第二天开工前,该企业按第一天的分配结果分配了5吨原材料后,又给 生产线分配了 吨原材料,给 生产线分配了 吨原材料.若两条生产线都能在一天内加工完各自分配到的所有原材料,且加工时间相同,则 的值为 .
如图,在 中, , , ,点 在边 上, ,联结 .如果将 沿直线 翻折后,点 的对应点为点 ,那么点 到直线 的距离为 .

如图,抛物线 与 轴交于点 ,点 ,与 轴交于点 ,且过点 .点 、 是抛物线 上的动点.
(1)求抛物线的解析式;
(2)当点 在直线 下方时,求 面积的最大值.
(3)直线 与线段 相交于点 ,当 与 相似时,求点 的坐标.
