观察等式: , , , ,已知按一定规律排列的一组数: , , , , ,若 ,用含 的代数式表示这组数的和是 .
如图1,菱形 的对角线 与 相交于点 , 、 两点同时从 点出发,以1厘米 秒的速度在菱形的对角线及边上运动.点 的运动路线为 ,点 的运动路线为 .设运动的时间为 秒, 、 间的距离为 厘米, 与 的函数关系的图象大致如图2所示,当点 在 段上运动且 、 两点间的距离最短时, 、 两点的运动路程之和为 厘米.

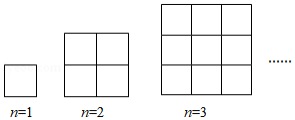
如图中的三个图形都是边长为1的小正方形组成的网格,其中第一个图形有 个小正方形,所有线段的和为4,第二个图形有 个小正方形,所有线段的和为12,第三个图形有 个小正方形,所有线段的和为24,按此规律,则第 个网格中所有线段的和为 (用含 的代数式表示)
如图,正方形 的对角线相交于点 ,点 在边 上,点 在 的延长线上, , 交 于点 , , ,则 .

如图,在 中, , 为 的中点, 平分 交 于点 , , 分别与 , 交于点 , ,连接 , ,则 的值为 ;若 ,则 的值为 .

2021年5月7日,《科学》杂志发布了我国成功研制出可编程超导量子计算机“祖冲之”号的相关研究成果.祖冲之是我国南北朝时期杰出的数学家,他是第一个将圆周率 精确到小数点后第七位的人,他给出 的两个分数形式: (约率)和 (密率).同时期数学家何承天发明的“调日法”是程序化寻求精确分数来表示数值的算法,其理论依据是:设实数 的不足近似值和过剩近似值分别为 和 (即有 ,其中 , , , 为正整数),则 是 的更为精确的近似值.例如:已知 ,则利用一次“调日法”后可得到 的一个更为精确的近似分数为: ;由于 ,再由 ,可以再次使用“调日法”得到 的更为精确的近似分数 现已知 ,则使用两次“调日法”可得到 的近似分数为 .
如图,在 中, , , ,点 是平面内一个动点,且 , 为 的中点,在 点运动过程中,设线段 的长度为 ,则 的取值范围是 .

如图,在正方形 中,点 、 分别在边 、 上,且 , 交 于 点, 交 于 点.
(1)若正方形的边长为2,则 的周长是 .
(2)下列结论:① ;②若 是 的中点,则 ;③连接 ,则 为等腰直角三角形.其中正确结论的序号是 (把你认为所有正确的都填上).

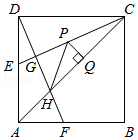
如图,正方形 中, ,连接 , 的平分线交 于点 ,在 上截取 ,连接 ,分别交 , 于点 , ,点 是线段 上的动点, 于点 ,连接 .下列结论:① ;② ;③ ;④ 的最小值是 ,其中正确结论的序号是 .
人们把 这个数叫做黄金分割数,著名数学家华罗庚优选法中的0.618法就应用了黄金分割数.设 , ,得 ,记 , , , ,则 .
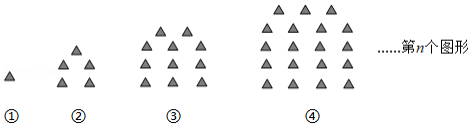
下面各图形是由大小相同的三角形摆放而成的,图①中有1个三角形,图②中有5个三角形,图③中有11个三角形,图④中有19个三角形 依此规律,则第 个图形中三角形个数是 .
在边长为4的正方形 中,连接对角线 、 ,点 是正方形边上或对角线上的一点,若 ,则 .