初中数学四种命题及其关系解答题

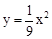如图①，在平面直角坐标系中，点P（0，m²）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C₁：于点A、B，交抛物线C₂：于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
【猜想与证明】
填表：

m	1	2	3

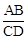由上表猜想：对任意m（m＞0）均有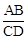=　 　．请证明你的猜想．
【探究与应用】
（1）利用上面的结论，可得△AOB与△CQD面积比为　 　；
（2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C₂于点E，过点D作y轴的平行线交抛物线C₁于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为　 　．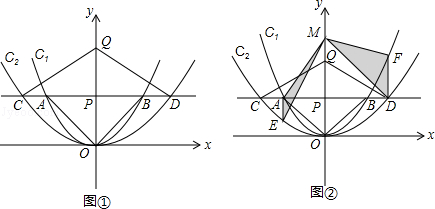

图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在每个网格中标注了5个格点．按下列要求画图：
（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；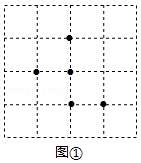

（2）在图②中，以格点为顶点，画一个正方形，使其内部已标注的格点只有3个，且边长为无理数．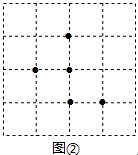

（本题6分）如图，已知一次函数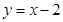与反比例函数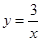的图象交于A、B两点．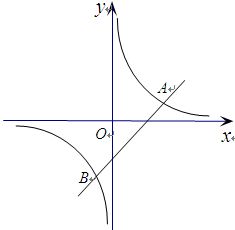

（1）求A、B两点的坐标；
（2）观察图象，请直接写出一次函数值小于反比例函数值的的取值范围．

已知某种水果的批发单价与批发量的函数关系如图（1）所示．
（1）请说明图中①、②两段函数图象的实际意义；

（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的函数关系式；在下图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多数量的该种水果；

（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，且当日零售价不变，请你帮助该经销商设计进货和销售的方案，使得当日获得的利润最大．

使得函数值为零的自变量的值称为函数的零点。例如，对于函数，令y=0，可得x=1，我们就说1是函数的零点。
己知函数 (m为常数)。
（1）当=0时，求该函数的零点；
（2）证明：无论取何值，该函数总有两个零点；
（3）设函数的两个零点分别为和，且，此时函数图象与x轴的交点分别为A、B(点A在点B左侧)，点M在直线上，当MA+MB最小时，求直线AM的函数解析式。

小明某天上午9时骑自行车离开家，15时回家，他有意描绘了离家的距离与时间的变化情况（如图所示）

（1）10时和13时，他分别离家多远?
（2）他到达离家最远的地方是什么时间?离家多远?
（3）他由离家最远的地方返回时的平均速度是多少?

如图，正方形ABCD的边长为2cm，在对称中心O处有一钉子.动点P、Q同时从点A出发，点P沿A→B→C方向以每秒2cm的速度运动，到点C停止，点Q沿A→D方向以每秒1cm的速度运动，到点D停止.P、Q两点用一条可伸缩的细橡皮筋联结，设x秒后橡皮筋扫过的面积为ycm².
当0≤x≤1时，求y与x之间的函数关系式；
当橡皮筋刚好触及钉子时，求x值
当1≤x≤2时，求y与x之间的函数关系式，并写出橡皮筋从触及钉子到运动停止时∠POQ的变化范围；
当0≤x≤2时，请在给出的直角坐标系中画出y与x之间的函数图象.

某企业为武汉计算机产业基地提供电脑配件，受美元走低的影响，从去年1至9月，该配件的原材料价格一路攀升，每件配件的原材料价格y₁（元）与月份x（1≤x≤9，且x取整数）之间的函数关系如下表：

月份x	1	2	3	4	5	6	7	8	9
价格y1（元/件）	560	580[	600	620	640	660	680	700	720

随着国家调控措施的出台，原材料价格的涨势趋缓，10至12月每件配件的原材料价格y₂（元）与月份x（10≤x≤12，且x取整数）之间存在如图所示的变化趋势：

请观察题中的表格，用所学过的一次函数、反比例函数或二次函数的有关知识，求出y₁与x之间的函数关系式，根据如图所示的变化趋势，求出y₂与x之间满足的一次函数关系式；
若去年该配件每件的售价为1000元，生产每件配件的人力成本为50元，其它成本30元，该配件在1至9月的销售量p₁（万件）与月份x满足函数关系式p₁=0.1x+1.1（1≤x≤9，且x取整数）10至12月的销售量p₂（万件）与月份x满足函数关系式p₂=﹣0.1x+2.9（10≤x≤12，且x取整数）．求去年哪个月销售该配件的利润最大，并求出这个最大利润；

使得函数值为零的自变量的值称为函数的零点．例如，对于函数，令，可得，我们就说是函数的零点．请根据零点的定义解决下列问题：已知函数（k为常数）．当k=2时，求该函数的零点；

某公司生产一种新型节能电水壶并加以销售，现准备在甲城市和乙城市两个不同地方按不同销售方案进行销售，以便开拓市场．
若只在甲城市销售，销售价格为y（元/件）、月销量为x（件），y是x的一次函数

月销量x（件）	1500	2000
销售价格y（元/件）	185	180

成本为50元/件，无论销售多少，每月还需支出广告费72500元，设月利润为（元）
（利润=销售额－成本－广告费）．若只在乙城市销售，销售价格为200元/件，受各种不确定因素影响，成本为a元/件（a为常数，40≤a≤70），当月销量为x（件）时，每月还需缴纳x²元的附加费，设月利
润为（元）（利润=销售额－成本－附加费）．
当x=1000时，y=    ▲  元/件，w_甲=   ▲   元
分别求出，与x间的函数关系式（不必写x的取值范围）；
当x为何值时，在甲城市销售的月利润最大？若在乙城市销售月利润的最大值与在甲城市销售月利润的最大值相同，求a的值；
如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在甲城市还是在乙城市销售才能使所获月利润较大？

某企业研发生产一种套装环保设备，计划_每套成本不高于50万元，且每月的产量不超过40套．已知这种设备的_月产量x（套）与每套的售价（万元）之间满足关系式，_月产量x（套）与生产总成本（万元）存在如图所示的一次函数关系.

求与x之间的函数关系式；
求月产量x的范围；
当月产量x（套）为多少时，这种设备的利润W（万元）最大

为丰富同学们的课余生活，学校将组织一次外出旅游活动，甲乙两家旅行社都提出优惠条件，甲旅行社表示每人都打八折，乙旅行社表示领队的20名教师免费，学生一律打九折，两家旅行社的报价都是每人300元。
请你写出两家旅行社所收总旅行费y（元）与学生人数x之间的函数关系。
为节省费用，你将选择哪家旅行社，请说出理由

如图所示，在直角坐标平面内，函数的图象经过A(1，4)，B(a，b)，其中a>1．过点A作x轴垂线，垂足为C，过点B作y轴垂线，垂足为D，连结AD、DC、CB．

若△ABD的面积为4，求点B的坐标
求证：DC∥AB
四边形ABCD能否为菱形？如果能，请求出四边形ABCD 为菱形时，直线AB的函数解析式；如果不能，请说明理由．

．已知函数，其中表示当时对应的函数值，即．
（1）求；
（2）计算的值；
（3）如果，试求的值．

下面的图象记录了某地一月份某天的温度随时间变化的情况，请你仔细观察图象回答下面的问题：

⑴　20时的温度是         ℃，温度是0℃的时刻是        时，最暖和的时刻
是        时，温度在－3℃以下的持续时间为      小时.
⑵　你从图象中还能获取哪些信息（写出3～4条即可）？