初中数学四种命题及其关系试题

若方程是关于x的一元二次方程，则必有（      ）

A．

B．一根为1

C．一根为－1

D．以上都不对

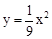如图①，在平面直角坐标系中，点P（0，m²）（m＞0）在y轴正半轴上，过点P作平行于x轴的直线，分别交抛物线C₁：于点A、B，交抛物线C₂：于点C、D．原点O关于直线AB的对称点为点Q，分别连接OA，OB，QC和QD．
【猜想与证明】
填表：

m	1	2	3

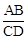由上表猜想：对任意m（m＞0）均有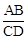=　 　．请证明你的猜想．
【探究与应用】
（1）利用上面的结论，可得△AOB与△CQD面积比为　 　；
（2）当△AOB和△CQD中有一个是等腰直角三角形时，求△CQD与△AOB面积之差；
【联想与拓展】
如图②过点A作y轴的平行线交抛物线C₂于点E，过点D作y轴的平行线交抛物线C₁于点F．在y轴上任取一点M，连接MA、ME、MD和MF，则△MAE与△MDF面积的比值为　 　．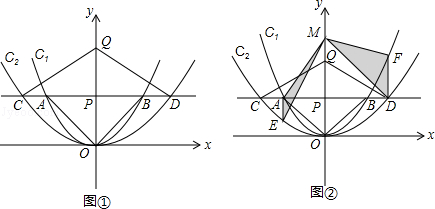

图①、图②都是4×4的正方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．在每个网格中标注了5个格点．按下列要求画图：
（1）在图①中以格点为顶点画一个等腰三角形，使其内部已标注的格点只有3个；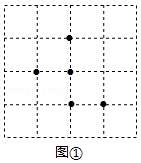

（2）在图②中，以格点为顶点，画一个正方形，使其内部已标注的格点只有3个，且边长为无理数．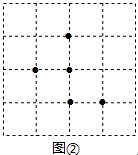

如下图，已知某容器是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成，若往此容器中注水，设注入水的体积为y，高度为x，则y关于x的函数图像大致是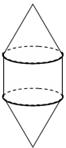
 

A．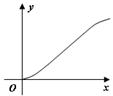

B．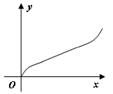

C．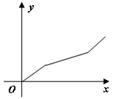

D．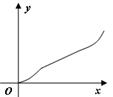

下列四个函数图象中，当x＞0时，y随x的增大而增大的是

如图，在平行四边形ABCD中，∠A=60°，AB=6厘米，BC=12厘米，点P、Q同时从 顶点A出发，点P沿A→B→C→D方向以2厘米/秒的速度前进，点Q沿A→D方向以1厘米/秒的速度前进，当Q到达点D时，两个点随之停止运动．设运动时间为x秒，P、Q经过的路径与线段PQ围成的图形的面积为y（cm²），则y与x的函数图象大致是（　　）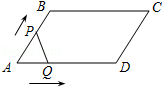

A．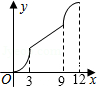

B．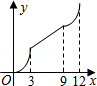

C．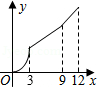

D．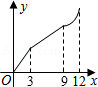

（本题6分）如图，已知一次函数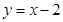与反比例函数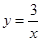的图象交于A、B两点．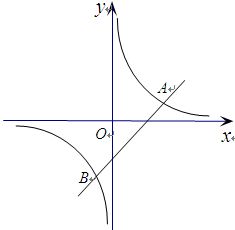

（1）求A、B两点的坐标；
（2）观察图象，请直接写出一次函数值小于反比例函数值的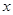的取值范围．

如图，AC=BC,点D是以线段AB为弦的圆弧的中点，AB=4，点E是线段CD上任意一点，点F是线段AB上的动点，设AF=x，AE²－FE²=y，则能表示y与x的函数关系的图象是（   ）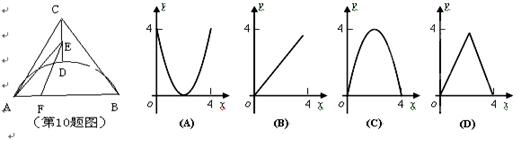

如图，AB是半圆O的直径，点P从点O出发，沿线段OA－弧AB－线段BO的路径匀速运动一周．设运动时间为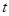，则下列图形能大致刻画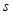与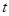之间关系的是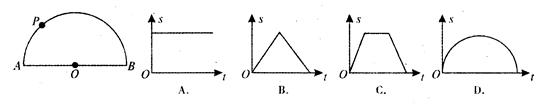

如图(1)，在直角梯形ABCD中，AB∥CD，∠ABC＝90º，动点P从点B出发沿BC，CD运动至点D停止．设点P运动的路程为x，△ ABP的面积为y，如果y关于x的函数图象如图(2)所示，则△BCD的面积是（    ）

A．3

B．4

C．5

D．6

下列函数中，当x＜0时，函数值y随x的增大而增大的有【   】
①y=x    ②y=－2x＋1         ③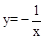       ④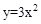

A．1个

B．2个

C．3个

D．4个

如图，在边长为4的正方形ABCD中，动点P从A点出发，以每秒1个单位长度的速度沿AB向B点运动，同时动点Q从B点出发，以每秒2个单位长度的速度沿BC→CD方向运动，当P运动到B点时，P、Q两点同时停止运动．设P点运动的时间为t，△APQ的面积为S，则S与t的函数关系的图象是【   】

为了建设社会主义新农村，我市积极推进“行政村通畅工程”．张村和王村之间的道路需要进行改造，施工队在工作了一段时间后，因暴雨被迫停工几天，不过施工队随后加快了施工进度，按时完成了两村之间的道路改造．下面能反映该工程已改造的道路里程y（公里）与时间x（天）的函数关系的大致图象是（　　）

如图，平面直角坐标系中，在边长为1的正方形ABCD的边上有一动点P沿运动一周，则P的纵坐标y与点P走过的路程s之间的函数关系用图象表示大致是                    

如图，A、B、C、D为⊙O的四等分点，动点P从圆心O出发，沿O — C — D — O路线作匀速运动．设运动时间为t（s），∠APB=y（°），则下列图象中表示y与t之间函数关系最恰当的是