[江苏]2012届江苏省大丰市九年级第一次调研考试数学试卷
据相关报道,2011年江苏省GDP总值达到万亿元.将这个数据用科学记数法表示为
| A.5.3×103亿元 | B.5.3×104亿元 | C.5.3×105亿元 | D.5.3×106亿元 |
某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是
| A.众数是80 | B.中位数是75 | C.平均数是80 | D.极差是15 |
已知抛物线y=x2+x-1经过点P(m,5),则代数式m2+m+2006的值为
| A.2012 | B.2013 | C.2014 | D.2015 |
只用下列正多边形地砖中的一种,能够铺满地面的是( )
| A.正十边形 | B.正八边形 |
| C.正六边形 | D.正五边形 |
一次函数y=kx+b的图象如图所示,当x>4时,y的取值范围是
| A.y<-3 | B.y<3 | C.y>3 | D.y>-3 |

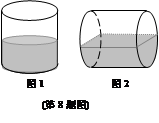
如图1所示,一只封闭的圆柱形水桶内盛了半桶水(桶的厚度忽略不计),圆柱形水桶的底面直径与母线长相等,现将该水桶水平放置后如图2所示,设图1、图2中水所形成的几何体的表面积分别为S 1、S 2,则S 1与S 2的大小关系是
| A.S1≤S 2 | B.S 1< S 2 | C.S 1> S 2 | D.S 1≥S 2 |
在四边形 中,对角线
中,对角线 与
与 互相平分,交点为
互相平分,交点为 .在不添加任何辅助线的前提下,要使四边形
.在不添加任何辅助线的前提下,要使四边形 成为矩形,还需添加一个条件,这个条件可以是 .
成为矩形,还需添加一个条件,这个条件可以是 .
为方便行人,打算修建一座高5米的过街天桥(如图所示),若天桥的斜面的坡度为i=1:1.5,则两个斜坡的总长度为______________米(结果保留根号)
如图,AB、AC都是圆O的弦,OM⊥AB,ON⊥AC,垂足分别为M、N,如果MN=3,那么BC=_________.
数学家们在研究15、12、10这三个数的倒数时发现: .因此就将具有这样性质的三个数称之为调和数,如6、3、2也是一组调和数.现有一组调和数:x、5、3(x>5),则x的值是 .
.因此就将具有这样性质的三个数称之为调和数,如6、3、2也是一组调和数.现有一组调和数:x、5、3(x>5),则x的值是 .
如图,在菱形ABCD中,E是AB的中点,且DE⊥AB.
求∠ABD的度数
若菱形的边长为2,求菱形的面积
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图:
求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
求图②中表示家长“无所谓”的圆心角的度数;
从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少
如图4,在梯形ABCD中,AD∥BC,AC⊥AB,AD=CD,cosB= ,BC=26.
,BC=26.
求:
cos∠DAC的值;
线段AD的长
有3张扑克牌,分别是红桃3、红桃4和黑桃5.把牌洗匀后甲先抽取一张,记下花色和数字后将牌放回,洗匀后乙再抽取一张.先后两次抽得的数字分别记为s和t,则︱s-t︱≥1的概率
甲、乙两人做游戏,现有两种方案.A方案:若两次抽得相同花色则甲胜,否则乙胜.B方案:若两次抽得数字和为奇数则甲胜,否则乙胜.请问甲选择哪种方案胜率更高?
如图,BD为⊙O的直径,AB=AC,AD交BC于点E.
①求证:△ABE∽△ADB;②若AE=2,ED=4,求⊙O的面积
延长DB到F,使得,连接FA,若AC∥FD,试判断直线FA与⊙O的位置关系,并说明理由.
如图所示,已知平面直角坐标系xOy,抛物线过点A(4,0)、B(1,3)
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线l,设抛物线上的点P(m,n)在第四象限,点P关于直线l的对称点为E,点E关于y轴的对称点为F,若四边形OAPF的面积为20,求m、n的值.
某土产公司组织20辆汽车装运甲、乙、丙三种土特产共120吨去外地销售.按计划20辆车都要装运,每辆汽车只能装运同一种土特产,且必须装满.根据下表提供的信息,解答以下问题:
| 土特产种类 |
甲 |
乙 |
丙 |
| 每辆汽车运载量(吨) |
8 |
6 |
5 |
| 每吨土特产获利(百元) |
12 |
16 |
10 |
设装运甲种土特产的车辆数为
 ,装运乙种土特产的车辆数为
,装运乙种土特产的车辆数为 ,求
,求 与
与 之间的函数关系式
之间的函数关系式如果装运每种土特产的车辆都不少于3辆,那么车辆的安排方案有几种?并写出每种安排方案.
若要使此次销售获利最大,应采用(2)中哪种安排方案?并求出最大利润的值
如图所示,在直角坐标平面内,函数的图象经过A(1,4),B(a,b),其中a>1.过点A作x轴垂线,垂足为C,过点B作y轴垂线,垂足为D,连结AD、DC、CB.
若△ABD的面积为4,求点B的坐标
求证:DC∥AB
四边形ABCD能否为菱形?如果能,请求出四边形ABCD 为菱形时,直线AB的函数解析式;如果不能,请说明理由.

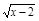 的自变量x的取值范围是_______________.
的自变量x的取值范围是_______________. (m为常数)有两个相等实数根,那么m=______.
(m为常数)有两个相等实数根,那么m=______.


 粤公网安备 44130202000953号
粤公网安备 44130202000953号