初中数学四种命题及其关系解答题

已知两个变量x、y满足关系2x-3y+1=0，试问：①y是x的函数吗？②x是y的函数吗？若是，分别写出y与x的关系式，若不是，说明理由．

已知二次函数图象的顶点坐标为M(1，0)，直线与该二次函数的图象交于A，B两点，其中A点的坐标为(3，4)，B点在轴上．
求m的值及这个二次函数的解析式；
若P(，0) 是轴上的一个动点，过P作轴的垂线分别与直线AB和二次函数的图象交于D、E两点．
①当0<< 3时，求线段DE的最大值；
②若直线AB与抛物线的对称轴交点为N，
问是否存在一点P，使以M、N、D、E
为顶点的四边形是平行四边形？若存在，
请求出此时P点的坐标；若不存在，请
说明理由．

设函数（为任意实数）
求证：不论为何值，该函数图象都过点（0，2）和（－2，0）；
若该函数图象与轴只有一个交点，求的值．

    
已知抛物线的解析式为
求抛物线的顶点坐标；
求出抛物线与x轴的交点坐标；
当x取何值时y>0？

(本题10分) 如图，直线与反比例函数的图象交于A，B两点．

（1）求、的值？
（2）直接写出时x的取值范围？
（3）如图，等腰梯形OBCD中，BC//OD，OB=CD，OD边在x轴上，过点C作CE
⊥OD于点E，CE和反比例函数的图象交于点P，当梯形OBCD的面积为12时，
请判断PC和PE的大小关系，并说明理由．

如图，以O为原点的直角坐标系中，A点的坐标为（0，3），直线x=-3交x轴于点B，P为线段AB上一动点，作直线PC⊥PO，交于直线x=﹣3于点C。过P点作直线MN平行于x轴，交y轴于M，交直线x=﹣3于点N。
（1）当点C在第二象限时，求证：△OPM≌△PCN；
（2）设AP长为m，以P、O、B、C为顶点的四边形的面积为S，请求出S与M之间的函数关系式，并写出自变量m的取值范围；
（3）当点P在线段AB上移动时，点C也随之在直线x=-3上移动，△PBC是否可能成为等腰三角形？如果可能，求出所有能使△PBC成为等腰三角形的点P的坐标，如果不可能，请说明理由。

 

黄冈市三运会期间，武穴黄商有一种姚明牌运动装每件的销售价y（元）与时间x（周）之间的函数关系式对应的点都在如图所示的图象上，该图象从左至右，依次是线段AB、线段BC、线段CD，而这种运动装每件的进价Z（元）与时间x（周）之间的函数关系式为Z=(1≤x≤16且x为整数)

（1）写出每件的销售价y（元）与时间x（周）之间的函数关系式；
（2）设每件运动装销售利润为w，写出w（元）与时间x（周）之间的函数关系式；
（3）求该运动装第几周出销时，每件运动装的销售利润最大？最大利润为多少？

（本小题满分8分）星期天，小明与小刚骑自行车去距家

50千米的某地旅游，匀速行驶1.5小时的时候，其中一
辆自行车出故障，因此二人在自行车修理点修车，用了
半个小时，然后以原速继续前行，行驶1小时到达目的
地．请在右面的平面直角坐标系中，画出符合他们行驶
的路程S（千米）与行驶时间t（时）之间的函数图象．

某厂从2001年起开始投入技术改进资金，经技术改进后，其产品的生产成本不断降低，具体数据如下表：

年   度	2001	2002	2003	2004
投入技改资金z(万元)	2.5	3	4	4.5
产品成本，(万元／件)	7.2	6	4.5	4

(1)请你认真分析表中数据，从你所学习过的一次函数、二次函数和反比例函数中确定哪种函数能表示其变化规律，说明确定是这种函数而不是其它函数的理由，并求出它的解析式；
(2)按照这种变化规律，若2005年已投人技改资金5万元．
①预计生产成本每件比2004年降低多少万元?
②如果打算在2005年把每件产品成本降低到3.2万元，则还需投入技改资金多少万元（结果精确到0.01万元)?

（本小题满分12分）如图，已知一次函数y＝kx＋b的图象交反比例函数
的图象于点A、B，交x轴于点C．
(1)求m的取值范围；
(2)若点A的坐标是(2，－4)，且＝，求m的值和一次函数的解析式．

如图，在平面直角坐标系中，一次函数y=kx+b（k≠0）的图象与反比例函数（m≠0）的图象相交于A、B两点．求：
（1）根据图象写出A、B两点的坐标并分别求出反比例函数和一次函数的解析式；
（2）根据图象写出：当x为何值时，一次函数值大于反比例函数值．

如图，正比例函数与反比例函数相交于A、B点．已知点A的坐标为A（4，n），BD⊥x轴于点D，且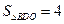．过点A的一次函数与反比例函数的图象交于另一点C，与x轴交于点E（5，0）．
（1）求正比例函数、反比例函数和一次函数的解析式；
（2）结合图象，求出当时的取值范围．

将一张矩形纸片沿对角线剪开(如图1)，得到两张三角形纸片、(如图2)，量得他们的斜边长为 6cm，较小锐角为30° ，再将这两张三角纸片摆成如图3的形状，且点 A、C、E、F 在同一条直线上，点 C 与点 E 重合， 保持不动，OB 为的中线，现对纸片进行如下操作时遇到了三个问题，请你帮助解决．
(1)将图3中的沿CA向右平移，直到两个三角形完全重合为止．设平移距离 CE 为 x(即 CE 的长)，求平移过程中，与重叠部分的面积 S 与 x 的函数关系式，以及自变量的取值范围；
(2) 平移到 E 与O 重合时(如图4)，将绕点 O 顺时针旋转，旋转过程中的斜边 EF交的 BC 边于 G，求点 C、O、G构成等腰三角形时，的面积；
(3)在(2)的旋转过程中， 的边 DE，EF分别交线段BC于点 G、H(不与端点重合)．求旋转角为多少度时，线段BH、GH、CG之间满足 , 请说明理由．

某同学从家里出发，骑自行车上学时，速度v（米/秒）与时间t（秒）的关系如图a，A（10，5），B（130，5），C（135，0）.
（1）求该同学骑自行车上学途中的速度v与时间t的函数关系式；
（2）计算该同学从家到学校的路程（提示：在OA和BC段的运动过程中的平均速度分别等于它们中点时刻的速度，路程＝平均速度×时间）；
（3）如图b，直线x＝t（0≤t≤135），与图a的图象相交于P、Q，用字母S表示图中阴影部分面积，试求S与t的函数关系式；
（4）由（2）（3），直接猜出在t时刻，该同学离开家所超过的路程与此时S的数量关系.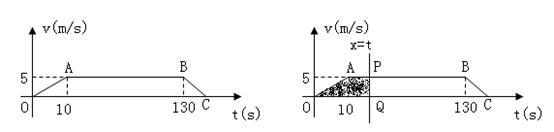

图a　　　　　　　　　　　　　　　　　　　　图b

在一条直线上依次有A、B、C三个港口，甲、乙两船同时分别从A、B港口出发，沿直线匀速驶向C港，最终达到C港．设甲、乙两船行驶x（h）后，与B港的距离分别为、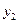（km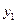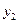），、与x的函数关系如图所示．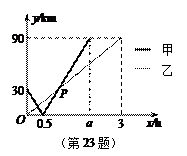

（1）填空：A、C两港口间的距离为    km，   ；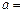
（2）求图中点P的坐标，并解释该点坐标所表示的实际意义；
（3）若两船的距离不超过10 km时能够相互望见，求甲、乙两船可以相互望见时x的取值范围．