2010年高级中等学校招生全国统一考试数学卷(湖北咸宁)
如图,将正方形ABCD中的△ABD绕对称中心O旋转至△GEF的位置,EF交AB于M,GF交BD于N.请猜想BM与FN有怎样的数量关系?并证明你的结论.
2010年,世博会在我国的上海举行,在网上随机调取了5月份中的某10天持票入园参观的人数,绘成下面的统计图.根据图中的信息回答下列问题:
(1)求出这10天持票入园人数的平均数、中位数和众数;
(2)不考虑其它因素的影响,以这10天的数据作为样本,估计在世博会开馆的184天中,持票入园人数超过30万人的有多少天?
8分)已知:关于x 的一元二次方程 的两根
的两根 满足
满足 ,双曲线
,双曲线 (x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求
(x>0)经过Rt△OAB斜边OB的中点D,与直角边AB交于C(如图),求 .
.
如图,⊙O的圆心在Rt△ABC的直角边AC上,⊙O经过C、D两点,与斜边AB交于点E,连结BO、ED,有BO∥ED,作弦EF⊥AC于G,连结DF.
(1)求证:AB为⊙O的切线;
(2)若⊙O的半径为5,sin∠DFE=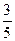 ,求EF的长.
,求EF的长.
国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价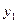 (万元)之间满足关系式
(万元)之间满足关系式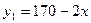 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本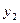 (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
(1)直接写出 与x之间的函数关系式;
与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
如图,直角梯形OABC的直角顶点O是坐标原点,边OA,OC分别在x轴、y轴的正半轴上,OA∥BC,D是BC上一点,BD= OA=
OA= ,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
,AB=3,∠OAB=45°,E、F分别是线段OA、AB上的两动点,且始终保持∠DEF=45°.
(1)直接写出D点的坐标;
(2)设OE=x,AF=y,试确定y与x之间的函数关系;
(3)当△AEF是等腰三角形时,将△AEF沿EF折叠,得到△ ,求△
,求△ 与五边形OEFBC重叠部分的面积.
与五边形OEFBC重叠部分的面积.
某校举行以“保护环境,从我做起”为主题的演讲比赛.经预赛,七、八年级各有一名同学进入决赛,九年级有两名同学进入决赛.前两名都是九年级同学的概率是 .
如图,小球从点A运动到点B,速度v(米/秒)和时间t(秒)的函数关系式是v=2t.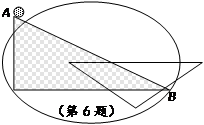
如果小球运动到点B时的速度为6米/秒,小球从点A到点B的时间是( ).
| A.1秒 | B.2秒 | C.3秒 | D.4秒 |
A、B、C、D四个班各选10名同学参加学校1 500米长跑比赛,各班选手平均用时及方差如下表:
| 班 |
A班 |
B班 |
C班 |
D班 |
| 平均用时(分钟) |
5 |
5 |
5 |
5 |
| 方差 |
0.15 |
0.16 |
0.17 |
0.14 |
各班选手用时波动性最小的是( ).
(A)A班 (B)B班 (C)C班 (D)D班
甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.
这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.
正确说法是( ).
| A.从甲箱摸到黑球的概率较大 |
| B.从乙箱摸到黑球的概率较大 |
| C.从甲、乙两箱摸到黑球的概率相等 |
| D.无法比较从甲、乙两箱摸到黑球的概率 |
如图,直线 与双曲线
与双曲线 相交于点A,点A的纵坐标为3,k的值为( ).
相交于点A,点A的纵坐标为3,k的值为( ).
| A.1 | B.2 | C.3 | D.4 |
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B.点M和点N分别是l1和l2上的动点,MN沿l1和l2平移.⊙O的半径为1,∠1=60°.下列结论错误的是( ).
(A) (B)若MN与⊙O相切,则
(B)若MN与⊙O相切,则
(C)若∠MON=90°,则MN与⊙O相切 (D)l1和l2的距离为2
在“抛掷正六面体”的试验中,如果正六面体的六个面分别标有数字“1”、“2”、“3”、“4”、“5”和“6”,如果试验的次数增多,出现数字“1”的频率的变化趋势是___________.
如果方程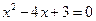 的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为_______.
的两个根分别是Rt△ABC的两条边,△ABC最小的角为A,那么tanA的值为_______.
一家鞋店对上周某一品牌女鞋的销售量统计如下:
| 尺码/厘米 |
22 |
22.5 |
23 |
23.5 |
24 |
24.5 |
25 |
| 销售量/双 |
1 |
2 |
5 |
11 |
7 |
3 |
1 |
该鞋店决定本周进该品牌女鞋时多进一些尺码为23.5厘米的鞋,影响鞋店决策的统计量是
| A.平均数 | B.众数 | C.中位数 | D.方差 |
平面直角坐标系中,点A的坐标为(4,3),将线段OA绕原点O顺时针旋转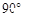 得到
得到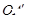 ,则点
,则点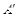 的坐标是
的坐标是
A.( ,3) ,3) |
B.( ,4) ,4) |
C.(3, ) ) |
D.(4, ) ) |
如图,两圆相交于A,B两点,小圆经过大圆的圆心O,点C,D分别在两圆上,若 ,则
,则 的度数为
的度数为
A. |
B. |
C. |
D. |
已知抛物线 (
( <0)过A(
<0)过A( ,0)、O(0,0)、
,0)、O(0,0)、
B( ,
, )、C(3,
)、C(3, )四点,则
)四点,则 与
与 的大小关系是
的大小关系是
A. > > |
B.  |
C. < < |
D.不能确定 |
如图,菱形ABCD由6个腰长为2,且全等的等腰梯形镶嵌而成,则线段AC的长为
| A.3 | B.6 | C. |
D. |
某学校为了解学生大课间体育活动情况,随机抽取本校100名学生进行调查.整理收集到的数据,绘制成如图所示的统计图.若该校共有800名学生,估计喜欢“踢
毽子”的学生有 人.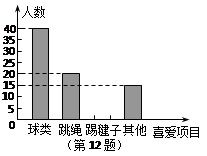
如图,已知直线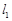 ∥
∥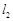 ∥
∥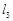 ∥
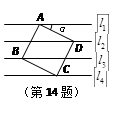
∥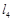 ,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则
,相邻两条平行直线间的距离都是1,如果正方形ABCD的四个顶点分别在四条直线上,则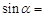 .
.
惠民新村分给小慧家一套价格为12万元的住房.按要求,需首期(第一年)付房款3万元,从第二年起,每年应付房款0.5万元与上一年剩余房款的利息的和.假设剩余房款年利率为0.4%,小慧列表推算如下: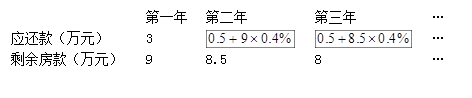
若第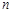 年小慧家仍需还款,则第
年小慧家仍需还款,则第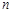 年应还款 万元(
年应还款 万元(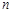 >1).
>1).
如图,一次函数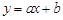 的图象与
的图象与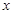 轴,
轴,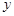 轴交于A,B两点,与反比例函数
轴交于A,B两点,与反比例函数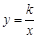 的图象相交于C,D两点,分别过C,D两点作
的图象相交于C,D两点,分别过C,D两点作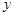 轴,
轴,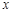 轴的垂线,垂足为E,F,连接CF,DE.
轴的垂线,垂足为E,F,连接CF,DE.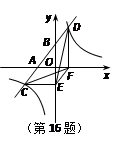
有下列四个结论:
①△CEF与△DEF的面积相等; ②△AOB∽△FOE;
③△DCE≌△CDF; ④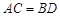 .
.
其中正确的结论是 .(把你认为正确结论的序号都填上)
随着人们节能意识的增强,节能产品的销售量逐年增加.某商场高效节能灯的年销售量2008年为5万只,预计2010年将达到7.2万只.求该商场2008年到2010年高效节能灯年销售量的平均增长率.
已知二次函数 的图象与
的图象与 轴两交点的坐标分别为(
轴两交点的坐标分别为( ,0),(
,0),( ,0)(
,0)( ).
).
(1)证明 ;
;
(2)若该函数图象的对称轴为直线 ,试求二次函数的最小值.
,试求二次函数的最小值.
如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,
将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若 ,求CD的长.
,求CD的长.
某联欢会上有一个有奖游戏,规则如下:有5张纸牌,背面都是喜羊羊头像,正面有2张是笑脸,其余3张是哭脸.现将5张纸牌洗匀后背面朝上摆放到桌上,若翻到的纸牌中有笑脸就有奖,没有笑脸就没有奖.
(1)小芳获得一次翻牌机会,她从中随机翻开一张纸牌.小芳得奖的概率是 .
(2)小明获得两次翻牌机会,他同时翻开两张纸牌.小明认为这样得奖的概率是小芳的两倍,你赞同他的观点吗?请用树形图或列表法进行分析说明.
问题背景
(1)如图1,
中,
分别交
,
于
,
两点,过点
作
交
于点
.请按图示数据填空:

四边形
的面积
△EFC的面积
△ADE的面积
探究发现
(2)在(1)中,若
,
,
与
间的距离为
.请证明
拓展迁移
(3)如图2,
的四个顶点在△ABC的三边上,若
、
、
的面积分别为2、5、3,试利用(2)中的结论求
的面积.

在一条直线上依次有A、B、C三个港口,甲、乙两船同时分别从A、B港口出发,沿直线匀速驶向C港,最终达到C港.设甲、乙两船行驶x(h)后,与B港的距离分别为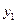 、
、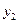 (km),
(km),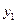 、
、 与x的函数关系如图所示.
与x的函数关系如图所示.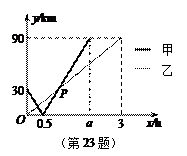
(1)填空:A、C两港口间的距离为 km,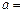 ;
;
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)若两船的距离不超过10 km时能够相互望见,求甲、乙两船可以相互望见时x的取值范围.
如图,直角梯形ABCD中,AB∥DC,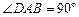 ,
,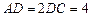 ,
,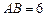 .动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).
.动点M以每秒1个单位长的速度,从点A沿线段AB向点B运动;同时点P以相同的速度,从点C沿折线C-D-A向点A运动.当点M到达点B时,两点同时停止运动.过点M作直线l∥AD,与线段CD的交点为E,与折线A-C-B的交点为Q.点M运动的时间为t(秒).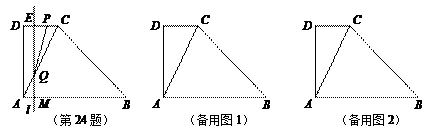
(1)当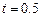 时,求线段
时,求线段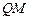 的长;
的长;
(2)当0<t<2时,如果以C、P、Q为顶点的三角形为直角三角形,求t的值;
(3)当t>2时,连接PQ交线段AC于点R.请探究 是否为定值,若是,试求这个定值;若不是,请说明理由.
是否为定值,若是,试求这个定值;若不是,请说明理由.









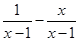 结果是( ).
结果是( ). 有意义的x取值范围是______.
有意义的x取值范围是______.
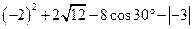
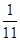
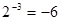
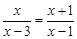 的解为
的解为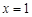
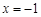
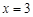
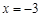
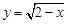 的自变量
的自变量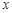 的取值范围是 .
的取值范围是 .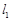 :
: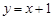 与直线
与直线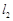 :
: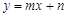 相交于点P(
相交于点P(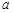 ,2),
,2),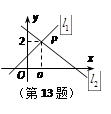
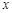 的不等式
的不等式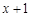 ≥
≥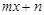 的解集为 .
的解集为 . ,其中
,其中
 粤公网安备 44130202000953号
粤公网安备 44130202000953号