国家推行“节能减排,低碳经济”政策后,某环保节能设备生产企业的产品供不应求.若该企业的某种环保设备每月的产量保持在一定的范围,每套产品的生产成本不高于50万元,每套产品的售价不低于90万元.已知这种设备的月产量x(套)与每套的售价 (万元)之间满足关系式
(万元)之间满足关系式 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本 (万元)存在如图所示的函数关系.
(万元)存在如图所示的函数关系.
(1)直接写出 与x之间的函数关系式;
与x之间的函数关系式;
(2)求月产量x的范围;
(3)当月产量x(套)为多少时,这种设备的利润W(万元)最大?最大利润是多少?
相关知识点
推荐套卷
 点坐标;
点坐标;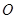 为旋转中心,将△ABC绕点
为旋转中心,将△ABC绕点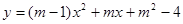 的图象经过原点,且开口向上.
的图象经过原点,且开口向上.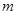 的值;
的值; 取什么值时,
取什么值时,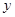 随
随
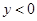 ?
?
 粤公网安备 44130202000953号
粤公网安备 44130202000953号