如图,△ABC在方格纸中.
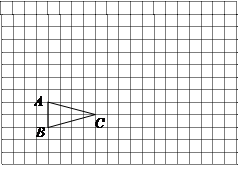
(1)请在方格纸上建立平面直角坐标系,使A(-5,-1),C(-1,-2),并求出
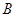 点坐标;
点坐标;
(2)以原点
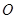 为旋转中心,将△ABC绕点
为旋转中心,将△ABC绕点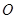 逆时针旋转90º得到△A’B’C’.请在图中画出△A’B’C’,并写出点A’,B’,C’的坐标.
逆时针旋转90º得到△A’B’C’.请在图中画出△A’B’C’,并写出点A’,B’,C’的坐标.
(3)以原点
 为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A’’B’’C’’.
为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A’’B’’C’’.
相关知识点
推荐套卷
如图,△ABC在方格纸中.
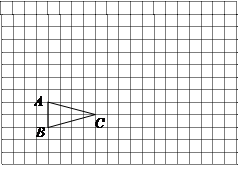
(1)请在方格纸上建立平面直角坐标系,使A(-5,-1),C(-1,-2),并求出
 点坐标;
点坐标;
(2)以原点
 为旋转中心,将△ABC绕点
为旋转中心,将△ABC绕点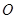 逆时针旋转90º得到△A’B’C’.请在图中画出△A’B’C’,并写出点A’,B’,C’的坐标.
逆时针旋转90º得到△A’B’C’.请在图中画出△A’B’C’,并写出点A’,B’,C’的坐标.
(3)以原点
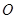 为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A’’B’’C’’.
为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A’’B’’C’’.