问题背景
(1)如图1,
中,
分别交
,
于
,
两点,过点
作
交
于点
.请按图示数据填空:

四边形
的面积
△EFC的面积
△ADE的面积
探究发现
(2)在(1)中,若
,
,
与
间的距离为
.请证明
拓展迁移
(3)如图2,
的四个顶点在△ABC的三边上,若
、
、
的面积分别为2、5、3,试利用(2)中的结论求
的面积.

相关知识点
推荐套卷




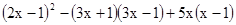 ,再选取一个你喜欢的数代替x,并求原代数式的值.
,再选取一个你喜欢的数代替x,并求原代数式的值. 粤公网安备 44130202000953号
粤公网安备 44130202000953号