如下图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置，设BC＝1，AC＝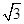
，则顶点A运动到点A″的位置时．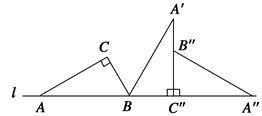
求：(1)点A经过的路线的长度；
(2)点A经过的路线与直线l所围成的面积(计算结果保留π)．
相关知识点
推荐套卷
如下图，把直角三角形ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B″C″的位置，设BC＝1，AC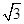＝，则顶点A运动到点A″的位置时．
求：(1)点A经过的路线的长度；
(2)点A经过的路线与直线l所围成的面积(计算结果保留π)．
粤公网安备 44130202000953号