[江苏]2012届江苏盐城盐都区九年级下学期期中质量检测数学试卷.
太阳的直径约为1390000千米,1390000用科学记数法表示为
| A.0.139×107 | B.1.39×106 | C.13.9×105 | D.139×104 |
如图,已知∠1 = 70º,如果CD∥BE,那么∠B的度数为

| A.70º | B.100º | C.110º | D.120º |
已知⊙O1与⊙O2的直径分别是4cm和6cm,O1O2=5cm,则两圆的位置关系是
| A.外离 | B.外切 | C.相交 | D.内切 |
下列说法正确的是
A.在一次抽奖活动中,“中奖的概率是 ”表示抽奖100次就一定会中奖 ”表示抽奖100次就一定会中奖 |
| B.随机抛一枚硬币,落地后正面一定朝上 |
| C.同时掷两枚均匀的骰子,朝上一面的点数和为6 |
D.在一副没有大小王的扑克牌中任意抽一张,抽到的牌是6的概率是 |
如图,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为 ,△ABP的面积为
,△ABP的面积为 ,如果
,如果 关于
关于 的函数图象如图所示,那么△ABC的面积是 ▲ .
的函数图象如图所示,那么△ABC的面积是 ▲ .

如图,以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO1,再以BE为对角线作第三个正方形EFBO2,如此作下去,…,则所作的第n个正方形的面积 = ▲ .
= ▲ .
在□ABCD中,E、F分别是AB、CD的中点,连接AF、CE.
求证:△BEC≌△DFA;
连接AC,当CA=CB时,判断四边形AECF是什么特殊四边形?并证明你的结论
水是人类宝贵的资源,节约用水应从我做起,从身边小事做起.小刚在他所在班的50名同学中,随机调查了10名同学家庭中一年的月平均用水量(单位:t),并将调查结果绘成了如下的条形统计图.
求这10个样本数据的平均数、众数和中位数
根据样本数据,估计小刚所在班50名同学家庭中月平均用水量不超过7 t的约有多少户.
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
| 朝下数字 |
1 |
2 |
3 |
4 |
| 出现的次数 |
16 |
20 |
14 |
10 |
计算上述试验中“4朝下”的频率是_________
根据试验结果,投掷一次正四面体,出现2朝下的概率是
 .”的说法正确吗?为什么?
.”的说法正确吗?为什么?随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
太阳能热水器具有安全、节能、环保、经济等优点.随着人们生活条件的不断改善,越来越多的太阳能热水器走进了普通人家.图1是安装在斜屋面上的热水器,图2是安装该热水器的侧面示意图.已知,斜屋面的倾斜角为30°,长为2米的真空管AB与水平线AD的夹角为45°,安装热水器的铁架水平横管BC长 米,求:
米,求:
真空管上端B到AD的距离(结果保留根号)
铁架垂直管CE的长(结果保留根号)
某企业研发生产一种套装环保设备,计划每套成本不高于50万元,且每月的产量不超过40套.已知这种设备的月产量x(套)与每套的售价 (万元)之间满足关系式
(万元)之间满足关系式 ,月产量x(套)与生产总成本
,月产量x(套)与生产总成本 (万元)存在如图所示的一次函数关系.
(万元)存在如图所示的一次函数关系.
求
 与x之间的函数关系式;
与x之间的函数关系式;求月产量x的范围;
当月产量x(套)为多少时,这种设备的利润W(万元)最大
问题提出
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小,而解决问题的策略一般要进行一定的转化,其中“作差法”就是常用的方法之一.所谓“作差法”:就是通过作差、变形,并利用差的符号确定他们的大小,即要比较代数式M、N的大小,只要作出它们的差M-N,若M-N>0,则M>N;若M-N=0,则M=N;若M-N<0,则M<N.
问题解决
如图1,把边长为a+b(a≠b)的大正方形分割成两个边长分别是a、b的小正方形及两个矩形,试比较两个小正方形面积之和M与两个矩形面积之和N的大小.
解:由图可知:M=a2+b2,N=2ab.
∴M-N=a2+b2-2ab=(a-b)2.
∵a≠b,∴(a-b)2>0.
∴M-N>0.
∴M>N.
类比应用已知:多项式M =2a2-a+1 ,N =a2-2a.试比较M与N的大小.
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边
满足a <b < c ,现将△ABC 补成长方形,使得△ABC的两个顶
点为长方形的两个端点,第三个顶点落在长方形的这一边的对边上。
①这样的长方形可以画 个;
②所画的长方形中哪个周长最小?为什么?
拓展延伸
已知:如图,锐角△ABC (其中BC为a,AC为b,AB为c)三边满足a <b < c ,画其BC边上的内接正方形EFGH , 使E、F两点在边BC上,G、H分别在边AC、AB上,同样还可画AC、AB边上的内接正方形,问哪条边上的内接正方形面积最大?为什么?

 的图象在
的图象在
 (x≠0且x≠-1),
(x≠0且x≠-1), ,
, ,…,
,…, ,则
,则 等于
等于 

 = ▲
= ▲ 

 有两个不等实根,则实数a的取值范围是 ▲
有两个不等实根,则实数a的取值范围是 ▲  ,则圆锥的侧面积是 ▲ .
,则圆锥的侧面积是 ▲ .
 在反比例函数
在反比例函数 的图象上,则
的图象上,则 ▲
▲  ,则∠A的度数为 ▲ .
,则∠A的度数为 ▲ .
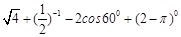
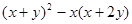
 .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号