如图，已知在平面直角坐标系xOy中，直角梯形OABC的边OA在y轴的正半轴上，OC在x轴的正半轴上，OA=AB=2，OC=3，过点B作BD⊥BC，交OA于点D．将∠DBC绕点B按顺时针方向旋转，角的两边分别交y轴的正半轴、x轴的正半轴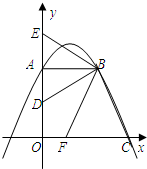
求经过A、B、C三点的抛物线的解析式；
当BE经过（1）中抛物线的顶点时，求CF的长；
在抛物线的对称轴上取两点P、Q（点Q在点P的上方），且PQ=1，要使四边形BCPQ的
周长最小，求出P、Q两点的坐标
相关试题
（本小题9分）如图，在所给网格图（每小格均为边长是1的正方形）中完成下列各题：
（1）作出格点
关于直线DE对称的
；（2）作出
绕点
顺时针方向旋转90°后
的
；（3）求
的周长．
，求
的值。
.(本小题7分)
相关知识点
推荐套卷
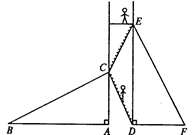
粤公网安备 44130202000953号